NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/01/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Botanique
Débutants Général	Phyllotaxie			Glossaire Général
INDEX Sciences	Botanique	Végétaux	Feuilles
	Phyllotaxie	Vocabulaire	Maths	Références
		Historique	Arithmétique	Géométrique
		Physique	Chimique	Numérique
		Sommaire de cette page >>> Vocabulaire >>> Notions mathématiques en phyllotaxie >>> Références

Phyllotaxie – Vocabulaire

Lexique des principaux termes à connaitre pour aborder la phyllotaxie.

Notions mathématiques impliquées en phyllotaxie

Références générales en phyllotaxie et références particulières ayant servies pour réaliser ces pages.

Vocabulaire
Morphogénèse	Regroupe toutes les études s’intéressant à la création de formes dans la Nature, vivante comme inerte; un champ de recherche tant expérimental que théorique. Du grec: création de formes (morpho: forme).
Morphologie	Étude des formes et des structures en soi. La morphogénèse étudie les facteurs qui les élaborent et les produisent.
Phyllotaxie	Ordre dans lequel sont implantées les feuilles ou les rameaux sur la tige d’une plante ainsi que les éléments d'un fruit, d'une feuille, d'un bourgeon ou d'un capitule. Science étudiant ces dispositions. Du grec ancien phyllon, feuille et taxis, arrangement, ordre).
Entropie	Mesure le désordre d'un système, de la matière ou de l'énergie. >>>
Téléologie	Étude de la finalité. Doctrine visant l'explication des phénomènes par l'intervention d'une cause finale (le telos). La téléologie s'oppose à la vision mécaniste de l’explication des phénomènes, notamment au sein des sciences du vivant. En phyllotaxie, cette théorie de la cause finale a été abandonnée avec l'arrivée de la théorie de l'évolution de Darwin.

Cycle foliaire	Quantité de feuilles rencontrées sur une tige ou un rameau, comptée depuis l'une de ces feuilles jusqu'à celle qui la surmonte exactement, et divisée éventuellement par 2 s'il a fallu faire deux tours pour le parcourir.
Méristème	La minuscule zone active qui se trouve au milieu des bourgeons dont le centre est l'apex. Ensemble de cellules indifférenciées et qui conservent la possibilité de se diviser, à l’origine de l’ensemble des tissus et des organes en croissance chez les végétaux. Les méristèmes permettent aux plantes de croître. Du grec meristos , «partager».
Un primordium Des primordia	Les primordia sont des renflements à la surface du méristème. Zone de forte activité de reproduction accompagnée de phénomènes de différenciation cellulaire. Les primordia se forment à intervalles réguliers (le plastochrone), à la même distance du centre de l'apex. Puis, ils se développent rapidement, tout en s'éloignant progressivement de l'apex. Selon le principe de la première place disponible, un nouveau primordium apparaîtrait chaque fois que les primordia précédents auraient libéré une place suffisante.
Apex; apical	Lieu de formation des primordia. Le méristème apical. MAC: méristème apical caulinaire. Anglais, SAM: Shoot Apical Meristem. Zone de croissance de la partie aérienne des végétaux. Il est composé de couches (L1 et L2 pour la tunique et L3 pour le corps). MAR: méristème apical racinaire. RAM: Root Apical Meristem. Zone de croissance des racines chez les végétaux.
Plastochrone	Temps qui sécoule entre l'initiation d'une feuille et la suivante (apparaition de deux nœuds successifs dans la génèse d'une tige. À chaque platochrone, un ou plusieurs primordia apparait là où il peut.

Spirale	Courbe qui est formé par un point qui se déplace en tournant autour d'un point en s'en éloignant de plus en plus. >>> Les spirales de développement des primordia sont logarithmiques. >>>
Spirale génétique, génératrice, générative, phyllotaxique	Ligne qui passe par chacun des nœuds consécutifs dans un mouvement de vis autour de la tige. Aussi: spirale ontogénique (ontos, être ou individu et genia, production, naissance).
Verticille	Ensemble de pièces, feuilles par exemple, implantées sur un axe au même niveau.
Parastique	Spirale parallèle qui relie les feuilles lors de leur apparition sur la tige, deux parastiques reliant les feuilles deux à deux, trois parastiques les reliant trois à trois, etc. Parastique droite ou dextre ou dextrogyre ou rétrograde: qui s'enroute dans le sens horaire. Parastique gauche ou senestre ou lévogyre ou directe: qui s'enroule dans le sens trigonométrique. Parastiche: nom italien (origine) et aussi anglais. On le trouve aussi en français.
Théorème fondamental de la phyllotaxie	Ce théorème indique l'écart entre angles de divergence compatible avec une structure phyllotaxique de type (m,n). Prouvé en utilisant différents modèles par Bravais, Adler, Jean, Hotton.

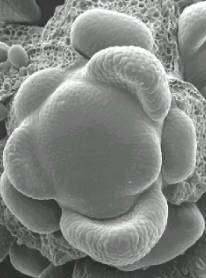
Nombre d'or (Phi) & Angle d'or (Alpha)	Observons les bourgeons d'une plante. Au niveau de la pointe, on y trouve une petite zone cônique, l’apex couvertes de protubérances, les primordia. Chaque primordium est la naissance d’un élément de la plante (fleur, feuille). Pour une majorité de plantes, l’angle entre deux primordia successifs et l’axe de la tige tend vers l'angle d'or. Suite >>>
Fibonacci	En référence à Leonardo Fibonacci(1170-1250) Suite de Fibonacci: 1, 1, 2, 3, 5, 8, 13… Nouveau = somme des due précédents. Fraction de Fibonacci: rapport entre deux nombres consécutifs comme 5/8. Cette fraction tend vers le nombre d'or. Quantité de parastiques (5, 8): souvent deux nombres consécutifs de la suite de Fibonacci. Suite >>>
Gradient	En gros: le taux de variation d'une grandeur. Gradient de concentration, gradient de croissance. En maths et en physique: une grandeur vectorielle indiquant la façon dont une grandeur physique varie dans l'espace. Notion voisine: pente, dérivée
Fraction phyllotaxique	Fraction avec au numérateur et dénominatueur deux nombres de Fibonacci consécutifs. Elle caractérise une plante. Chêne (2/5), amandier (5/13), etc.
Angle de divergence	Angle entre deux primordia successifs. Souvent observé comme proche de 137,5°, l'angle d'or.
Maillage en hélice	Disposition de points régulièrement espacés sur les cercles d'un cylidre à raison de un point par cercle et avec un angle de divergence constant entre points successifs. Anglais: helical lattice.
Maillage en spirale	Disposition de point sur des cercles concentriques dont le rayon augmente régulièrement et et avec un angle de divergence constant entre points successifs. Anglais: helical spiral. Elle peut être obtenue en utilisant les puissancesentières d'un seul nombre complexe. Voir Règle d'Hofmeister

Notions mathématiques utiles en phyllotaxie

Algèbre des nombres complexes Arbre de Cayley (Tables de Cayley) Arbre de Farey Arbre de Stern-Brocot (représentation de tous les rationnels strictement positifs, sous forme de fractions irréductibles). Bifurcations (fractales) Domaine géométrique de Dirichlet (lieu des points du réseau plan les plus proches d'un point donné comparés aux autres) Équations différentielles et résolution numérique (ordinateurs) Fractions de Farey Géométrie cartésienne et polaire Géométrie hyperbolique (triangle curviligne) Gradient Loi de probabilité de Fisher Optimisation (recherche d'extremum) Problèmes de remplissage compact de sphères Réseaux sur cylindre (cylindrical lattices) Spirale logarithmique Statistiques et notamment expérimentation par plan d'expérience (carrés latins) Suite de Fibonacci et de Lucas

Phyllotaxie – Références

Introduction Plantes, spirales et nombres – Vidéo introductive sur la phyllotaxie - Département mathématiques et du département biologie de l'Université de Fribourg L'arithmétique des plantes – Futura mathématiques (5 pages) Nombre d'or dans la nature Scolaires (TPE) Phyllotaxie spirale – TPE - ALBERTIN Thierry - CAVALLARO Jean-Sébastien - MARCHESE Emilie 1ère S3 La croissance des plantes Générales Phyllotaxie – Wikipédia Introduction à la morphogénèse (1) – Ocochet – 2011 Spirales végétales et maillage dynamique – JPM Chabert – Le site scientifique de référence Méthode de Turing et morphogénèse : illustration des équations de réaction-diffusion - El Mellah Ileyk, Loh Alan, Pottier Alizée Générales (anglais) Fibonacci Numbers and Nature – Ron Knott Avancées Croissance végétale et morphogénèse – Roger V. Jean – Masson – 1983 Formes, figures et réalités – Gérard Chazal – 1997 Le destin des formalismes: à propos de la forme des plantes – Pratiques et épistémologies des modèles face à l'ordinateur – Franck Varenne – 2005 – 837 pages Morphogénèse végétale, Phyllotaxie – Jérôme Chopard – INRIA – 2008 – Planches d'un diaporama de thèse. Avanceés (anglais) Phyllotaxis – Maths.smith.edu – Site anglais dédié à ce sujet A History of the Study of Phyllotaxis – I. Adler, D. Barabe et R.V. Jean – 1996 Airy and Schwendener – Classic geometric models in phyllotaxis – Les schémas de la modélisation de Schwendener – Sur le site Phylllotaxis - The fundamental theorem of phyllotaxis – Jonathan Swinton – 2012 How much number theory do you have to know to be a sunflower – Leonid Levitov (MIT) – 2007 – Modélisation expliquée relativement simplement Symmetry in Plants – Roger V. Jean et Denis Barabé – 1998 Auxine, agent secret de la croissance A plausible model of phyllotaxis – Smith et al. The Turing Archives – The chemical basis of morphogenesis – 1951 Magnetic cactus experimentally demonstrates mathematical plant patterns – Lisa Zyga - 2009

Suite	Phyllotaxie – Historique Phyllotaxie – Développements: point de vue arithmétique
Voir	Atomes Biologie – Index Carbone Chlorophylle et magnésium Dualité Éléments chimiques Formation de l'oxygène Particules Respiration humaine
Livre	Le Nombre d'or – Marius Cleyet-Michaud – puf Que sais-je – 1973
Site	Voir références ci-dessus
Cette page	http://villemin.gerard.free.fr/aScience/Botanique/PhylVoca.htm