|
|||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Phyllotaxie – Développements Le point de vue physique, mécanistique Principales
hypothèses expliquant l'arrangement doré des feuilles ou fleurs et approches
mathématiques. Cette page
aborde les tentatives d'explications de la structure si particulière des
pantes: feuilles ou fleurs. Cette page est faite pour tous ceux qui
voudraient toucher du doigt le domaine de la phyllotaxie explicative.
Autrement-dit, il s'agit d'une approche simplifiée (simpliste). Toute erreur
d'interprétation serait de mon fait. |
|
Phyllotaxie –
Interprétations |
|
|
|
Espace libre |
Chaque
feuille primordiale naît dans le plus grand espace libre immédiatement
disponible entre les deux feuilles précédentes. (Hofmeister
– 1868) |
|
|
Évolution |
La
divergence entre feuilles consécutives est telle que les feuilles
optimisent l'exposition à la lumière
tout en facilitant leur transpiration. (Wiesner –
1875) |
|
|
Contraintes |
Champ de
tension (contraintes biophysiques) qui naît autour des primordia, contrôlant
la position du nouveau primordium. (Schwendener –
1878) |
|
|
Équipotentielles |
L'énergie
vitale se comporterait comme l'énergie électrique. Le spirales seraient les
équipotentielles. (Church – 1904) |
|
|
Densité |
Les
primordia se rangent de façon dense autour d'un cylindre. Modèle identique à
celui de la pression de contact
engendré par la croissance. (Van Iterson –
1907). Première tentative pour expliquer le rangement doré. |
|
|
Pression de contact |
Chaque
feuille croit en diamètre jusqu'à ce quelle touche sa voisine le plus proche,
après quoi elle essaie de grandir. (Adler – 1974) |
|
|
Premier espace |
Une théorie
mixte, très souple, connue sous le nom de théorie du premier espace
disponible, a été élaborée par M. et R. Snow au cours d'une longue série de
recherches expérimentales (1931-1962) : l'action d'un facteur mécanique
(l'espace disponible) est modulée par les inhibitions. |
|
|
Énergie de répulsion |
Maximalisation
de l'énergie de répulsion. (Levitov – 1991): billes
densément réparties autour d'un cylindre avec croissance sous contraintes
(stress) anisotropiques (croissance axiale lente et
radiale rapide, comme observée chez les plantes). Levitov
(MIT) conclut qu'avec ce modèle la phyllotaxie dorée est expliquée. Douady et Couder (1996) >>> |
|
|
Synthèse |
"Explications basées sur des notions de
physique, toutes plus ou moins équivalentes à la théorie d'Adler : la
stabilité des structures type Fibonacci est due à la pression de contact, ou
à une élasticité des tissus tendant à favoriser les assemblages les plus
compacts, ou à une croissance différentielle tendant à rééquilibrer la
densité du réseau, etc." Selon JPM. Chabert |
|
|
|
|||
|
|
|
||
|
|
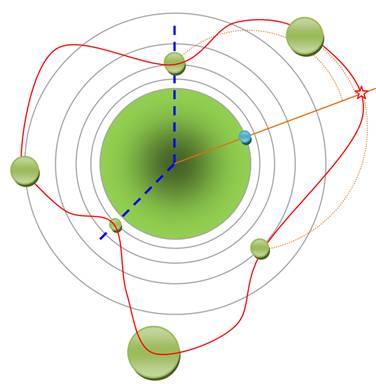
Une
itération est caractérisée par:
|
||
|
Naissance d'un primordium (bleu) Les primordium existants sont visualisés en vert
sur les cercles de croissance
(imaginaires). Pour tous les rayons (ici en marron), on
considère le point sur le cercle intérieur (bleu). On mesure la distance aux primordia voisins (arc
de cercle en pointillés marron). On conserve la plus grande distance (étoile
rouge). La courbe rouge montre le lieu de tous ces points de plus grande
distance. La règle d'Hofmeister
dit que le nouveau primordium (bleu) va naitre au point de plus grande
distance maximum (étoile rouge). Ce mode de croissance, sous certaines conditions
sur le facteur de croissance, fait apparaître les primordia successifs avec
un angle de divergence voisin de 137,5° (pointillés bleus). |
|
||
Voir Exemples d'itérations successives sur
le site de math.smith.com
|
|
||
|
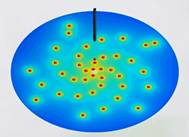
Des
chercheurs* ont réalisé ce modèle (photo): un axe et des disques
aimantés montés sur roulement à billes et libre de mouvement. À la
grande surprise des chercheurs, le dispositif vérifie la disposition des
feuilles prévu par Levitov (1991): maximalisation
de l'énergie de répulsion * Risoli et al. -
Los Alamos National Laboratory in New Mexico; Cornell University in Ithaca,
New York; and The Pennsylvania State University (PSU). |
|
|
|
|
||
|
La
meilleure modélisation actuelle est celle de Douady
et Couder (1996). C'est une simulation physique qui illustre le phénomène de
manière très intuitive. Elle est basée sur l'effet de l'énergie de répulsion. L'arrivée des graines est simulée par l'ajout régulier de gouttes d’un
fluide magnétique. La nouvelle arrive dans un champ de gouttes anciennes et subit leur
effet répulsif. Au fur et à mesure, le substrat est étiré pour simuler la croissance. La
simulation mathématique montre également, et de façon rigoureuse,
l’apparition des spirales et en quantité respectant la suite de Fibonacci.
Elle a été mené par Pau Atela,
Chris Golé et Scott Hotton. |
Voir Vidéo >>> |
|
|
De toutes ces interprétations physiques c'est celle basée sur l'effet
de l'énergie de répulsion qui semble donner le plus de satisfaction. La disposition des parastiques selon les nombres de Fibonacci et l'arrivée
des feuilles selon un angle d'or sont vérifiées de manière tangible. |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Botanique/PhylPhys.htm
|
![]()