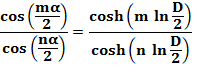|
|||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Phyllotaxie – Développements Vision géométrique Principales
hypothèses expliquant l'arrangement doré des feuilles ou fleurs et approches
mathématiques. Après la
période d'observation et de décompte, les botanistes cherchent à représenter
la structure des feuilles ou des fleurs à l'aide de dessins géométriques. Cette page est faite pour tous ceux qui
voudraient toucher du doigt le domaine de la phyllotaxie explicative.
Autrement-dit, il s'agit d'une approche simplifiée (simpliste). Toute erreur
d'interprétation serait de mon fait. |
|
|
||
|
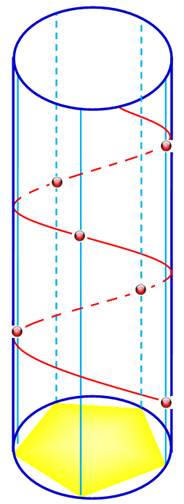
Cylindre (en position verticale pour la
compréhension). Une spirale plaquée sur le cylindre:
une hélice. Une
verticale (bleue clair) sur le
cylindre coupe l'hélice: nœuds de l'hélice (billes rouges) Si la
distance entre les nœuds reste constante, l'hélice est régulière. Cette distance entrenœuds est notée
e, le pas de l'hélice. L'écart
angulaire entre nœuds successifs est constant. C'est la divergence (div). On repère
un point sur l'hélice par:
Voir Réseaux
de Bravais / Coordonnées |
Que se passe-t-il si on resserre sur les spires, comme si on appuyait
sur un ressort? |
|
|
En
sélectionnant un point sur k points, on définit de nouvelles hélices, des
sous-hélices |
Avec un point sur deux => deux sous-hélices P0, P2, P4, P6, P8, P10, P12, P14,… P1, P3, P5, P7, P9, P11, P13, P15,… |
|
|
Quelle
est la sous-hélice la plus "serrée". Celle pour laquelle l’arc de
courbe joignant deux points successifs est le plus court. |
Parmi toutes ces sous-hélices, visuellement, il en existe une pour
laquelle la distance entre deux nœuds voisins est la plus courte. On l'a
nomme paristique actuelle. C'est celle qui
accroche le regard. Les autres sont dites potentielles. En tentant de réduire le pas entrenœuds, l'ordre des spires diffère.
Certaines de resserrent plus vite que d'autres. L'ordre d'actualisation est
caractéristique de la divergence de l'hélice. |
|
|
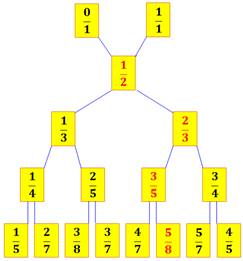
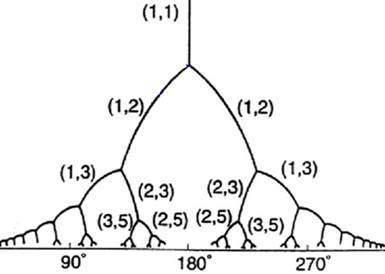
Le graphe
montre l'arbre de Farey.
L'analogie des spires de ressort qui se contractent peut se prolonger sur cet
arbre. Alors, on montre que les spires suivront un arrangement noté par les
fractions en rouge. Précisément, les fractions de Fibonacci, observées en
comptant les parastiques: 1/2, 2/3, 3:5, 5/8 … |
|
|
|
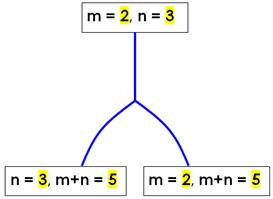
Pour
avoir une idée de ce qui se passe, imaginez les billes dans ce tube. En
les compressant par le haut, la bille
3 va se glisser entre les billes 1 et 2 jusqu'à
toucher la bille 0. Les
experts parlent de bifurcation. Le cheminement privilégie certaines billes
parents et adopte la séquence de
Fibonacci parmi toutes les possibilités de l'arbre de Farey. De ce
fait – contexte fibonaccien – l'angle de divergence
est bien l'angle d'or. De
nombreuses expérimentations dont le cactus
magnétique (Risoli et al.) montre que les angles
de divergence se stabilisent rapidement sur l'angle d'or. |
|
|
|
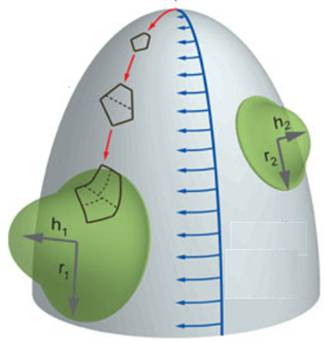
Comment
les primordia progressent-ils? Le schéma
donne une vision géométrique du méristème apical (gris) et de la croissance
des primordia (verts). La croissance
est symbolisée par les flèches:
La
croissance est caractérisée par le facteur gamma:
r est le
rayon du primordium (vert) et R est le rayon du cercle du méristème portant
le primordium. |
|
|
1907 van Iterson |
Modèle dense: les
primordia se rangent de façon dense autour d'un
cylindre. Modèle identique à celui de la pression de contact engendré par la croissance. Le premier a avoir tenté de comprendre leur lien profond avec la
suite de Fibonacci. Travaux méconnus
jusqu'en 1973 (Erikson). Son équation, avec alpha, angle de divergence, D
le diamètre des sphères placées autour du cylindre:
Sa résolution nécessite une série
d'approximations successives. Modélisation >>> |
|
|
||
|
Ce modèle
géométrique consiste à placer des billes une à une avec un angle constant. Selon la
valeur d l'angle, le taux de remplissage varie. Le
remplissage optimal est obtenu pour l'angle d'or. Ici, les
parastiques sont (21,34) |
|
|
|
|
||
|
On dessine un
réseau (un quadrillage) sur un cylinbre
sur lequel il sera commode de représenter les spirales (parastiques), les
espaces entre nœuds. Plaquer des disques
sur le cylindre de façon la plus dense n'explique par l'apparition des
nombres de Fibonacci. Par contre … En introduisant une
contrainte (interaction répulsive) pour la coissance, la structure subit une
déformation. On introduit
également une dissymétrie de croissance: lente selon l'axe et plus rapide sur
le rayon. Alors, les
embranchements (les bifurcations) s'organisent selon un arbre de Cayley
(proche de celui de Farey).
Les nombres de la suite de Fibonacci
y sont inclus. |
Implication des arbres de Caley 1) Construction
2) Effet constaté
|
|
|
Le
point de vue géométrique de la phyllotaxie
des feuilles sur une tige s'appuie sur une figuration du cylindre de la tige
développée sur un plan. L'enjeu est d'étudier les spirales (les parastiques)
et le comportant de ces spirales sous contraintes. Sous
certaines conditions de stress, l'arrangement des primordia s'aligne selon un
modèle doré: l'angle de divergence (angle entre deux feuilles successives)
est, alors, l'angle d'or. De plus, la quantité de spirales droites et celle
de spirales gauches sont des nombres de Fibonacci successifs. |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Botanique/PhylGeom.htm
|
![]()