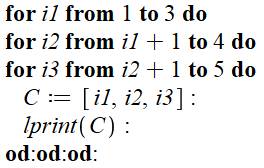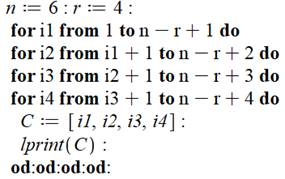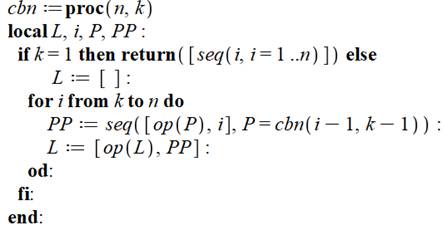|
||||||||||||||||||||||||||||
![]()
|
Combinaisons – Énumération Comment lister toutes les combinaisons de r objets parmi n ? Algorithme et programmation.
Exemple 10 parmi 100 conduit
à: 17 310 309 456 440, plus de treize mille milliards de combinaisons. À
raison de 10 combinaisons par ligne et 5 mm par ligne, il faut un papier long
de plus de huit millions de km (24 fois la distance
Terre-Lune). |
|
|
||
|
On se
propose d'écrire le programme qui liste les dix combinaisons de 3 parmi 5. |
Ensemble de n éléments L = [1, 2, 3, 4, 5] Énumération des combinaisons de 3 parmi 5 A1 = [1, 2, 3] A2 = [1, 2, 4] … A10 = [3, 4, 5] |
|
|
Avec le
logiciel Maple, la fonction est
présente. Notre but est de se passer de cette instruction et de
comprendre la logique d'énumération de ces combinaisons. |
|
|
|
|
||||
|
Petit programme simple
|
Principe de l'algorithme On traite d'abord le dernier nombre en
l'incrémentant dans la plage possible, soit de 3 à 5. On fait la même chose pour l'avant-dernier nombre
(ici le deuxième) en le traitant lui aussi dans la plage permise, soit de 2 à
4. Pour chaque valeur, on retraite le dernier nombre (boucle imbriquées). Idem pour le premier avec une nouvelle boucle
imbriquant les deux autres. Programme Trois boucles fonctionnant dans les plages
indiquées. Il suffit de prendre les trois index de boucles à
chaque fois pour les afficher. Ce sont les combinaisons dans l'ordre lexicographique. Elles sont affichées en bleu. |
|||
|
Traitement avec n quelconque
|
|
Commentaire Petite amélioration qui permet de traiter une liste initiale de
longueur n quelconque. Mais … Inconvénient, r est figé par la quantité de lignes que le programmeur
a introduite dans le programme. |
||
|
|
|||||
|
On
cherche les combinaisons de => Dont on prend r éléments => |
L = {1, 2, 3, … n} A = {a1, a2,
a3, … ar} |
||||
|
Ordre (lexicographique) |
A = {a1, a2,
a3, … ak …
ar} B = {b1, b2,
b3, … bk … br} On dit que: A < B si
ak < bk et tous les précédents sont égaux |
||||
|
Extrêmes |
Amin = {1,
2, 3, … r} Amax = {(n
– r + 1) …. (n – 1), n} Exemple pour n = 5 et r = 3 Amin = {1,
2, 3} Amax = {(5
– 3 + 1) …. (4), 5} = {3, 4, 5} |
||||
|
Successeur Voir le Graphe |
A = {a1, a2, a3,
… ak–1 , ak …
ar} Si A < Amax et ak Alors ASucc = {a1, a2, … ak–1 , (ak +1), (ak
+2) … (ak + r – k
+ 1)} Si le plus grand nombre n'est pas au max pour sa
position, on lui ajoute 1 et on complète avec les nombres successifs. Ainsi:
2347 devient 2356 Exemple pour n = 5 et r = 3 125 =>
5 est au max; 2 est le plus grand; il passe à 2 + 1 = 3 et le suivant prend la valeur suivante: 3 + 1 = 4 => 134. 134 =>
4 est le plus grand; il passe à 4 + 1 = 5; il n'y a pas de suivant =>135 135 =>
5 est au max; 3 est le plus grand; il passe à 3 + 1 = 4 et le suivant prend
la valeur suivante => 145. 145 =>
5 est au max; 4 est au max dans sa position; 1 est le plus grand; il passe à
1 + 1 = 2 et les suivants prennent la valeur suivante => 234. |
||||
|
Traitement avec l'index k selon la formule
indiquée |
A = {1, 2, 5} k = 3
=> n – r + k = 5 – 3 + 3 = 5 &
5 = 5 Non retenu k = 2
=> n – r + k = 5 – 3 + 2 = 4 &
4 => ak
= 2 => ASucc
= {1, 2+1, 2+3-2+1} = {1, 3, 4} A = {1, 3, 4} k = 3
=> n – r + k = 5 – 3 + 3 =5 & 4
=> ak
= 4 => ASucc
= {1, 3, 4 + 1 ou 4 – 3 + 3 + 1} = {1, 3, 5} |
||||
|
|
||||
|
La
construction de la liste des combinaisons obéit à deux lois générales:
Algorithme 1.
Former la combinaison: A = [1, 2, …r]. 2.
Si C est égale à la combinaison Amax FIN. 3.
Trouvez le plus grand k tel que ak est le plus grand sans
être à sa valeur maximale. 4.
Modifier A en faisant +1 sur ak et en mettant les nombres
suivants aux valeurs suivantes à partir de ak. 5.
Retourner en 2. Commentaire Cet
algorithme de type conventionnel n'est pas facile à implémenter. Sa
version récursive est plus adaptée. |
|
|||
|
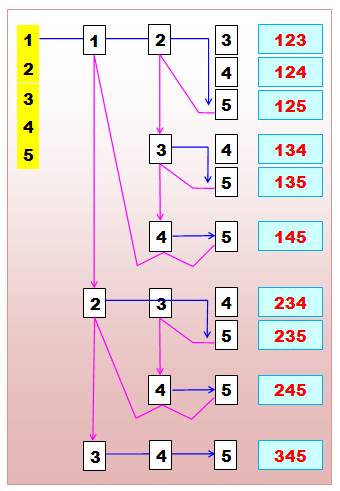
Algorithme récursif Il repose
sur la remarque suivante: chaque combinaison C(i, k) est issue de la
combinaison précédente C(i–1, k–1). |
C(3, 1) |
|
|
|
|
C (4, 2) |
|
|||
|
C(5,3) |
||||
|
|
|||
|
Une explication utile à la compréhension de la suite. Programmation des suites de nombres
|
Explications La première instruction est classique. C'est la
manière habituelle de créer une suite.
Ici, avec les crochets, on demande une liste.
La deuxième montre comment obtenir une suite de
listes de deux nombres. La troisième instruction montre comment on peut
inclure une suite dans une autre suite.
|
||
|
Programme d'énumération des combinaisons
|
Commentaire Deux parties:
Le programme est très concis. Il utilise:
Le programme principal montre deux exemples d'appel à la procédure. On
en profite pour donner la quantité de combinaisons. Résultats En bleu, les combinaisons selon deux exemples d'appel à la procédure. |
||
|
Variante
|
Pour information Une des suites est explicitée en utilisant une boucle. L'autre suite (PP : = seq) est conservée,
car bien difficile à rendre compte avec une boucle. |
||
Programme pour copie dans Maple
|
cbn := proc (n, k) if k = 1
then return [seq(i, i = 1 .. n)] else [seq(seq([op(P), i], P = cbn(i-1, k-1)), i = k .. n)]
end if end proc; %; #Programme
principal A := cbn(5, 3); q := nops(A); B
:= cbn(6, 4); q := nops(B); |
Voir Programmation – Index
|
|
Voir Anglais – Le bagage minimum
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()