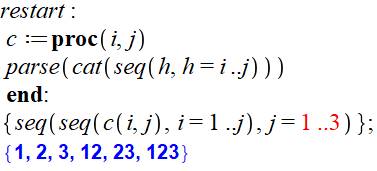|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES avec TOUS les chiffres Sommes pannumériques
ordonnées Quelles sont les sommes obtenues
en utilisant tous les chiffres dans l'ordre, y compris avec concaténations.
Toutes ces sommes sont des multiples de 9, mais pas tous les multiples de 9. Exemples
666 = 1
+ 2 + 3 + 4 + 567 + 89 = 123 + 456 + 78 + 9 |
Voir Nombre 123456789
|
|
|||
|
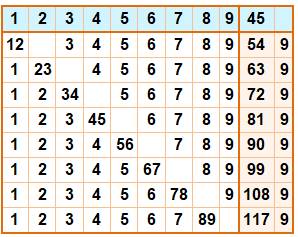
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (9 × 10) / 2 = 45 |
|||
|
Somme
avec une concaténation de 2. La
première avec 12 donne une somme de 54, soit celle des chiffres avev une
augmentation de 9 (en effet: 11 – 2 = 9). Les
suivantes incrémentent également le résultat précédent par 9. Toutes
ces sommes sont des multiples de 9. |
|
||
|
|
||
|
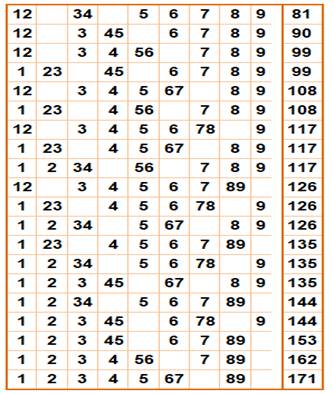
Cas de la
somme de tous les chiffres dans l'ordre et avec double concaténations. On
retrouve des sommes parmi celles vues plus haut, et certaines sommes sont
multiples. Liste des
nombres atteints par ce type de somme: Ces
nombres sont tout naturellement multiples de 9. En effet, comportant tous les
chiffres une seule fois, chacune a 9 pour racine
numérique. |
|
|
|
|
||
|
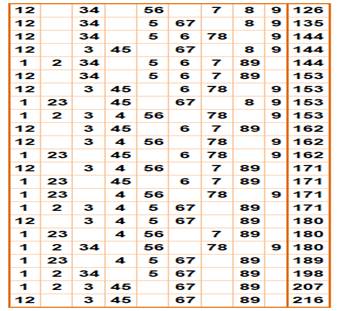
Cas de
triple concaténations. Mêmes
constats: multiplicité, tous les multiples de 9 à partir de 45. La liste
devient: {45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135,
144, 153, 162, 171, 180, 189, 198, 207} Tous les
multiples de 9 à partir de 45. Ce ne sera plus le cas ensuite. Les nombres
243, 297 …, ne sont pas accessibles avec une telle somme pannumérique. |
|
|
|
|
||
|
Nombres à chiffres concaténés Il y en a 45 |
1, 2, 3, 4, 5, 6, 7, 8, 9,
12, 23, 34, 45, 56, 67, 78, 89, 123, 234, 345, 456, 567, 678, 789, 1234, 2345,
3456, 4567, 5678, 6789, 12345, 23456, 34567, 45678, 56789, 123456, 234567,
345678, 456789, 1234567, 2345678, 3456789, 12345678, 23456789, 123456789 |
|
|
Nombres somme des chiffres concaténés Ils sont exactement 187 |
45, 54, 63,
72, 81,
90, 99, 108, 117,
126, 135, 144, 153, 162, 171, 180, 189, 198, 207, 216, 225, 234, 252, 261, 270,
279, 288, 315, 324, 333, 342, 378, 387, 396, 432, 441, 450, 459, 486, 495,
504, 513, 549, 558, 567, 576, 594, 603, 612, 621, 630, 666, 675, 684, 693,
702, 711, 720, 729, 738, 747, 756, 783, 810, 819, 828, 837, 846, 855, 864,
873, 882, 891, 927, 963, 972, 1035, 1044, 1080, 1143, 1152, 1251, 1260, 1269,
1314, 1323, 1332, 1341, 1368, 1377, 1386, 1395, 1818, 1890, 1926, 2034, 2079,
2376, 2430, 2439, 2448, 2502, 3033, 3141, 3483, 3492, 3546, 3555, 3564, 4248,
4257, 4590, 4599, 4608, 4662, 4671, 4680, 4707, 4779, 5697, 5706, 5715, 5724,
5733, 5814, 5922, 6804, 6813, 6822, 6831, 6840, 6849, 6858, 6921, 6957, 7029,
7137, 7146, 8028, 9135, 12375, 12429, 12438, 12447, 12501, 13032, 13140,
19134, 23481, 23544, 23553, 24246, 34587, 34596, 34659, 34668, 45693, 45702,
45711, 45810, 56799, 56808, 56817, 56826, 56835, 56916, 57024, 58023, 123480,
123543, 123552, 124245, 234585, 234657, 345690, 345699, 456795, 456804,
456813, 456912, 1234584, 1234656, 2345688, 3456792, 3456801, 12345687,
23456790. |
|
|
Multiples de 9 intouchables jusqu'à 2000 |
9, 18, 27, 36, 243,
297, 306, 351, 360, 369, 405, 414, 423, 468, 477, 522, 531, 540, 585, 639,
648, 657, 765, 774, 792, 801, 900, 909, 918, 936, 945, 954, 981, 990, 999,
1008, 1017, 1026, 1053, 1062, 1071, 1089, 1098, 1107, 1116, 1125, 1134, 1161,
1170, 1179, 1188, 1197, 1206, 1215, 1224, 1233, 1242, 1278, 1287, 1296, 1305,
1350, 1359, 1404, 1413, 1422, 1431, 1440, 1449, 1458, 1467, 1476, 1485, 1494,
1503, 1512, 1521, 1530, 1539, 1548, 1557, 1566, 1575, 1584, 1593, 1602, 1611,
1620, 1629, 1638, 1647, 1656, 1665, 1674, 1683, 1692, 1701, 1710, 1719, 1728,
1737, 1746, 1755, 1764, 1773, 1782, 1791, 1800, 1809, 1827, 1836, 1845, 1854,
1863, 1872, 1881, 1899, 1908, 1917, 1935, 1944, 1953, 1962, 1971, 1980, 1989,
1998, 2007, … |
|
Voir Brève
599
|
|
||
|
Programme Maple: nombres concaténés
Exemple Avec i = 2 et j = 5, on aurait: {2, 3, 4, 5, 12,
23, 34, 45, 123, 234, 345, 1234, 2345, 12345} |
But Créer la liste de tous les nombres concaténés de i à j (ici de 1 à 3).
Sorte de combinaisons, mais avec formation des nombres (et non liste). Procédure c(1, j) Création de la concaténation des nombre de i à j. Avec i = 1 et j = 3,
on aura 123. Programme principal Double séquence qui balaye les valeurs de i et j et appel de la
procédure pour la concaténation correspondante. |
|
|
Sommes des nombres concaténés
Exemple Avec i = 2 et j = 5, on aurait: |
But Calculer les sommes des nombres concaténés. Procédure S(i, j) Enchainement de trois séquences combinant les
paramètres (i, j, et h). Programmes récursif: il
fait appel deux fois à lui-même. L'instruction remember
indique que les résultats de calcul sont tabulés et n'ont pas à être refaits
lors d'un nouvel appel. Merveille de construction due à Alois P. Heinz,
en 2014. Voir OEIS A24226 Programme principal Appel de la procédure pour (1, 3). Évidemment, avec (1, 9), on obtient la liste des
187 nombres somme de chiffres (plus le nombre complet 123456789). |
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()