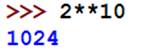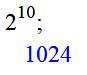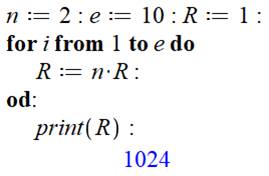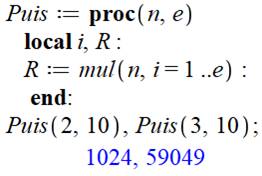Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 29/07/2025 M'écrire Brèves de Maths

INDEX Python Programmation Informatique Multimédia Ordinateur	Python – Comment se lancer et initiation
	INITIATION	BASES	MATHS
	Démarrer	Les classiques	Chiffres
	Exemple – pas à pas	Arithmétique	Palindrome
		Puissances

PROGRAMMATION PYTHON – Puissances & Récursivité Le calcul de la puissance d'un nombre est simple et la fonction existe dans tous les langages de programmation. Cette page présente un exercice de familiarisation avec la méthode de calcul récursive. Comment calculer une puissance en employant cette méthode ? Comment accélérer le calcul ?
	Sommaire de cette page >>> Calcul type calculette de la puissance d'un nombre >>> Programme simple de calcul de la puissance >>> Calcul de la puissance d'un nombre par récursivité >>> Petit théorème de Fermat et instruction pow (x,y,z)	Débutants Programmation Glossaire Informatique Algorithme

Voir absolument Mon espace de travail en Python

Calcul type calculette de la puissance d'un nombre
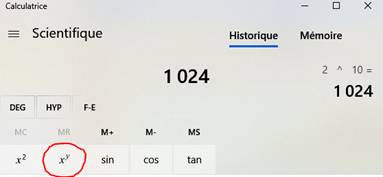
Les logiciels, tout comme les calculettes, disposent d'une fonction de calcul direct de la puissance (x^y).		Calculette de votre ordinateur
Python	Maple

Programme simple de calcul de la puissance
Sans la présence de la fonction puissance, comment calculer n à la puissance e.	On développe un algorithme qui multiple e fois n par lui-même.
Python	Maple
Python avec fonction (def)	Maple avec procédure (proc)
Notez la différence entre Python et Maple concernant le contrôle des bouches.
Pyhon compte les JALONS Il faut 11 jalons pour 10 intervalles. En Python on écrit (0, 10) ou alors (1, 11). Soit for i in range (0,e)	Pyhon compte les INTERVALLES Il faut 11 jalons pour 10 intervalles. En Maple on écrit (1, 10) ou alors (0, 9). Soit for i from 1 to e do

Merci à Enekio

Point de situation

Ce qui précède constitue une révision du codage en Python ou Maple.

Voyons maintenant, comment accélérer le calcul en utilisant la récursivité.

Voir Programmation – Index

Calcul de la puissance d'un nombre par récursivité
Le principe de cet algorithme rapide repose sur le fait qu'une puissance paire comporte des carrés de n et, une puissance impaire comporte, en plus, le facteur n.	Puissance paire: n^4 = n^2 x n^2 Puissance impaire: n^5 = n x n^2 x n^2
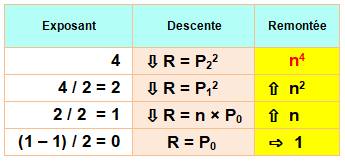
La récursivité fonctionne de la manière suivante, par exemple pour n^4: Descente Pour 4 (pair), le résultat R est égal au carré du résultat de la puissance divisée par 2. Pour 2 (pair), idem: R = résultat de la puissance divisé par 2, au carré. Pour 1 (impair), on multiplie le résultat de la puissance inférieure par n. Pour 0, le résultat vaut 1. 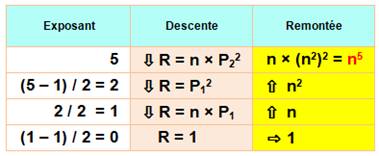Remontée Le programme a conservé les résultats intermédiaires en mémoire, et, en remontant, il remplace les résultats en attente par leur valeur: Sachant que pour 0, R = 1 Pour 1: R = n x 1 = n Pour 2: R = n^2 Pour 4: R = (n^2)^2 = n^4	Récursivité pour la puissance 4 Récursivité pour la puissance 5
Programme Python	Programme Maple

Petit théorème de Fermat et instruction pow(x,y,z)
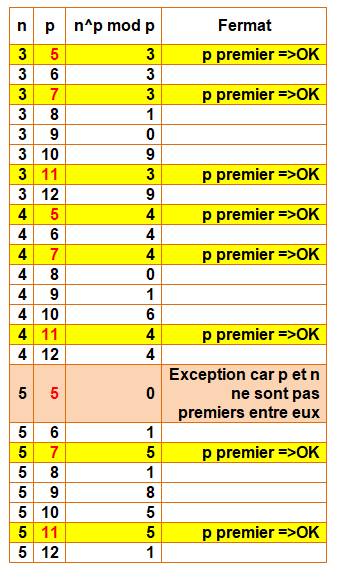
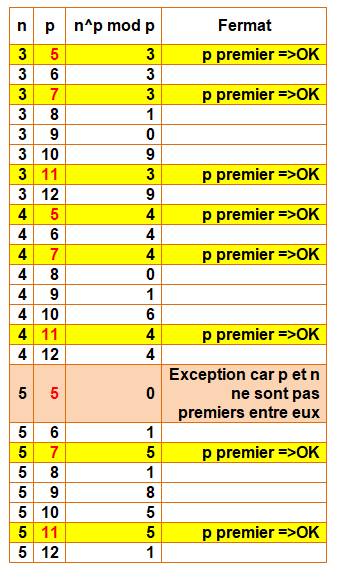
Petit théorème de Fermat Un nombre à une puissance première est égale au nombre modulo cette puissance. Programme Python Le programme calcule n^p mod p avec l'instruction pow (x, y, z) qui retourne x^y mod z. Résulats dans tableau ci-contre Il faut bien comprendre que le théorème offre une propriété pour les nombres p premiers (en rouge et jaune). La réciproque n'est pas vraie: ce n'est pas parce que la propriété est vérifiée que le nombre p est premier, il peut tout aussi bien être composé.

Voir Petit théorème de Fermat

Retour	Python – Ce qu'il faut absolument comprendre avant de se lancer
Suite	Mes premiers pas en arithmétique Tour d'horizon avec l'exemple des palindromes Mes premiers dessins
Voir	Scratch – Apprendre à programmer simplement Maple – Apprendre à programmer (maths) Historique de l’aventure informatique
Sites	Pensez en Python – Allen B. Downey – 2016 – Vous y trouverez les explications détaillées avec exemples de toutes les notions exposées dans cette page
Cette page	http://villemin.gerard.free.fr/aInforma/PYTHON/Puissan.htm