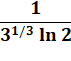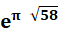|
|||||||||||||||||||||||||||||
![]()
|
NOMBRES PRESQUE ENTIERS
Du domaine de la récréation mathématique ou de l'amusement pour passionnées de nombres et de recherches systématiques sur ordinateurs, les nombres presque entiers trouvent souvent une explication profonde. Un nombre presque entier ne diffère d'un entier que d'une petite quantité comme en témoigne la quantité de zéros ou de neufs derrière la virgule. |
Voir Nombres décimaux
Explications
|
Le presque entier se présente en trois morceaux:
La lettre grecque Phi La plupart des nombres cités ont été trouvés par des passionnés. En majorité la référence au découvreur figure sur le site de Wolfram MathWorld.
|
Table avec des 0 après la virgule
|
0, |
99 |
99999 |
|
|
|
1, |
00 |
155160 |
|
|
|
31, |
00 |
627668 |
|
|
|
3, |
00 |
278070 |
|
|
|
1, |
000 |
308872 |
|
|
|
1, |
000 |
759099 |
|
|
|
3571, |
000 |
280033 |
|
|
|
9349, |
000 |
106963 |
|
|
|
0, |
0000 |
176734 |
|
|
|
109, |
0000 |
338701 |
|
|
|
86, |
0000 |
188810 |
|
|
|
927, |
0000 |
205934 |
|
|
|
2143, |
00000 |
274805 |
|
|
|
1, |
00000 |
970263 |
|
|
|
0, |
00000 |
278768 |
|
|
|
431, |
000000 |
407270 |
|
|
|
395, |
000000 |
536428 |
88 ln 89 |
|
|
1087, |
000000 |
204958 |
|
|
|
318, |
0000000 |
332526 |
|
|
|
0, |
0000000 |
366137 |
|
|
|
7, |
0000000 |
857367 |
|
|
|
E^19 064, |
00000000 |
856707 |
Trouvé par Anthony Canu en 2017 |
|
|
E^34, |
000000000 |
163738 |
|
|
|
163, |
0000…028 |
232167 |
|
|
|
E^30, |
0000…030 |
497498 |
|
|
|
119, |
0000…031 |
959374 |
|
|
![]()
Table avec des 9 après la virgule
|
0, |
99 |
417717 |
|
|
|
19, |
999 |
09997 |
|
|
|
9, |
999 |
838797 |
|
|
|
E^7, |
999 |
3411 |
|
|
|
5777, |
999 |
826929 |
|
|
|
0, |
999 |
766858 |
|
|
|
6530, |
9999 |
859900 |
|
|
|
0, |
99999 |
02066 |
– sin(11) |
|
|
31, |
99999 |
873849 |
|
|
|
E^11, |
999999 |
8222 |
|
|
|
0, |
999999999 |
24368 |
|
|
|
0, |
999999999 |
817034 |
cos(103 993) |
|
|
0, |
9999999999 |
848336 |
– sin(52 174) |
|
|
E^18, |
9999…912 |
2498 |
|
|
|
9999…914 |
8829 |
Trouvé par Anthony Canu en 2016 |
||
|
0, |
9999…916 |
7857 |
– sin(2017 |
|
|
E^21, |
9999….920 |
873748 |
|
|
|
E^30, |
9999…930 |
195029 |
Fib(360) / Fib(216) |
|
|
E^39, |
9999….938 |
671353 |
|
|
|
E^50, |
9999….938 |
671353 |
|
|
|
|
|
427,0000000000 0000000000 0000000000 0000000000 0000000001 06271… |
Source: Daniel Lignon – Dictionnaire de (presque) tous les nombres entiers
Général
|
Les nombres notés "Général" sont en quantité infinie, de même que leur quantité de 0 ou de 9. On donne un exemple (puissance 100), mais, augmenter la puissance et vous obtiendrez encore plus de 0 ou de 9 répétés. |
![]()
|
Retour |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()