|
|||||||||||||||||||||||||||||||||||
![]()
|
ou SUITE de SYRACUSE ____ Une introduction Comment aborder simplement
cette suite de nombres
tout en utilisant les outils tableur
et programmation (niveau
première). |
Oups! Je suis vraiment
débutant: Découverte Junior des cycles tels que
celui de Syracuse
Règle du
jeu
|
|
||
|
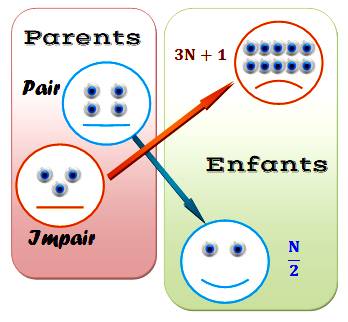
On nous
propose l'algorithme indiqué. Il
consiste à procéder à p itérations
et, pour chacune, à examiner le nombre N
tel a été initialisé ou calculé. Si N est pair, on le divise par 2 et si N est impair on le multiple par 3 et on ajoute 1. |
Algorithme Lire (p) Lire (N) Pour i entier allant de 1 à p faire Si N est
pair, alors N prend la valeur N/2 Fin de Si |
|
|
Cet
algorithme produit une suite de nombres, la suite de Syracuse (nom d'une
université aux États-Unis
>>>). Anodine dans sa définition, elle
présente de nombreuses surprises qui ont intéressé les mathématiciens. |
Cette suite fait l'objet d'une conjecture qui n'a
jamais été infirmée, mais pas démontrée non plus. Conjecture La suite de Syracuse finit
toujours pas arriver au nombre 1. |
|
|
|
||
|
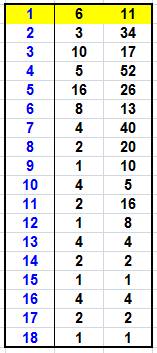
Voyons ce
qui se passe avec 18 itérations et en prenant N = 6 puis N = 11 comme nombres
initiaux. Tous calculs faits, les deux suites se
présentent comme indiqué dans ce tableau. Le nombre 6 est pair; son successeur est: 6 / 2 = 3; Le nombre 3 est impair, son
successeur est: 3x3 + 1 = 10 Etc. On
remarque un bouclage sur 4, 2, 1 … que l'on appelle le cycle trivial. De
là à penser que cette suite finit
toujours comme cela … Remarque tout départ N égal à une puissance de
2 atterrit direct sur ce cycle. |
…, 128, 64, 32, 16, 8, 4, 2, 1 |
|
Trivial est un synonyme de banal.
|
|
||||||||||||
|
Opérations successives à réaliser
|
Allure du tableur
Deux instructions imbriquées
Modulo Le modulo d'un nombre est le reste de
sa division par un nombre donné; en l'occurrence, ici, par 2. Il s'agit de
tester si le nombre est pair ou
impair. |
|||||||||||
|
|
||
|
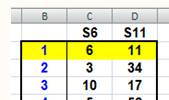
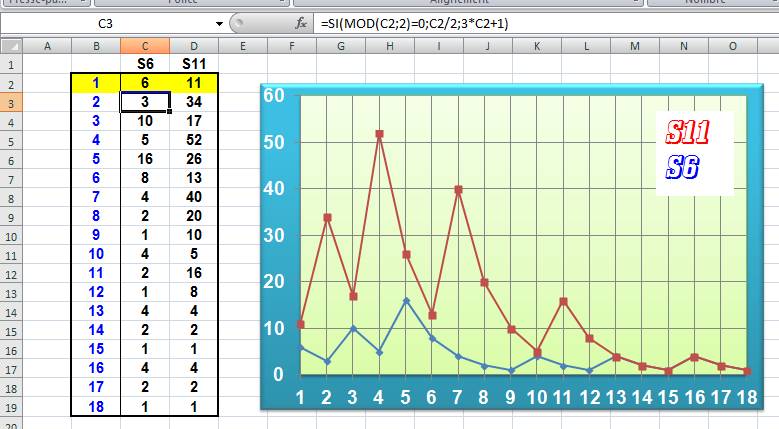
Tableau On donne
le tableur complet avec formule en C3 mise en évidence. |
Graphique Pour le graphique, faire " Insertion / Ligne" et choisir le
type de graphique. Détail: pour obtenir les abscisses bien en face: cliquez la zone des
abscisses, cliquez droit; mise en forme de l'axe; position de l'axe: sur les
graduations. |
|
|
|
||
|
|
||
|
Récurrence |
U0
= N (nombre entier au
choix) Si
Un est pair: Un+1
= Un / 2 Si
Un est impair: Un+1
= 3Un + 1 |
|
|
Temps de
vol: indice pour lequel la suite arrive à 1 pour la première fois. |
T6 = 9 T11
= 15 |
|
|
Altitude maximale: valeur maximale de la
suite de nombres. |
A6 = 16 A11
= 52 |
|
|
Exemple avec 27, un nombre remarquable par son temps de vol. |
T27
= 111 A27
= 9 232 |
|
Suite de
Syracuse pour n = 27 (la liste comporte 111 valeurs)
|
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322,
161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466,
233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668,
334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958,
479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911,
2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433,
1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53,
160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 |
Voir Commentaires sur cette suite
|
|
||
|
Programme
|
Commentaires Restart (redémarrer) réinitialise tout. Déclaration des valeurs de p (une valeur quelconque
qui assure que le cycle sera complet) et N avec le "deux points égal". Impression de la première valeur avec lprint. Mise en rouge d'une boucle: pour i de 2 à p faire
(for from to do). Condition avec if: si N est pair (son reste est nul
en divisant par 2), alors (then) on divise N par 2 et on replace cette valeur
dans la mémoire N. Sinon (else), la mémoire N est remplie avec la
valeur 3N + 1. Fin de condition (fi qui est le if à l'envers). Impression de N et de son rang (i). Puis, fin de boucle (od). En bleu, le résultat de l'impression. Remarques Ce programme traduit exactement l'algorithme
donné au départ, mais en anglais. En ce sens, il est abordable par tout
débutant. Il est également transposable sur un autre
logiciel que Maple. Spécificités Maple: Les instructions se terminent avec un : L'affectation (N prend la valeur …) est notée := |
|
Voir Suite de cette
programmation (temps de vol …) / Programmation
– Débutant / Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()