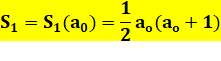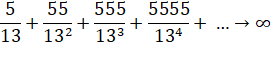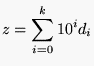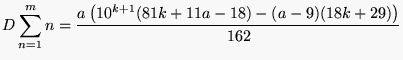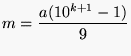NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 08/04/2024

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

       

IDENTITÉS

 

Débutants

Somme

SOMMES

 

Glossaire

Addition

 

INDEX

 

Narcissiques

Somme-Produit Ch

Formes et motifs

Nombres en chiffres

Chiffres

Sommes de nombres

Types de nombres

Jeux et énigmes

 

S. de nombres

S. de chiffres

S. des entiers

S. des impairs

S. de Nbs Démo.

S. de carrés

S. de cubes

S. de puissances

Narcissiques

N + Somme Ch

S. des Ch de nk

S. de factorielles

S. des nombres en 1234

 

Sommaire de cette page

>>> Se repérer

>>> Somme des chiffres des nombres de 1 à 100

>>> Curiosités

>>> Calcul de la somme cumulée des chiffres

>>> Records

>>> Programmation

>>> Somme des chiffres des nombres jusqu'à 99…

>>> Curiosités

>>> Formules

>>> Nombres dont la somme des chiffres est k

 

 

 

 

 

SOMME DES CHIFFRES des nombres

 

Fonction, curiosités et formule de calcul.

Voir: introduction sur la somme des chiffres.

Ne pas confondre avec la racine numérique (de la preuve par neuf).

 

Exemple

Définition

Fonction somme des chiffres:

   Sn = (… + m + c + d + u) – milliers, centaines, dizaines, unités

Fonction cumul de la somme des chiffres:

   CSn = S1 + S2 + … Sn = CS(n–1) + Sn

Voir Astuces tableur (somme des chiffres)

 

Anglais: digital sum or digsum

 

 

Se repérer …

Somme des chiffres

(cette page)

n = 1234

SC(n) = 1 + 2 + 3 + 4 = 10

Somme simple des chiffres
Une fonction arithmétique particulière

>>>

Racine numérique

n = 1234

RN(n) = 1

car 1 + 2 + 3 + 4 = 10 & 1 + 0 = 1

Somme répétée des chiffres
Base de la preuve par neuf

>>>

Racine numérique des multiples

m = 7

RNM (7)  = (7, 5, 3, 1, 8, 6, 4, 2, 9)

Cette suite se répète pour les multiples suivants de 7. Vrai pour tous les m.

>>>

Clé de divisibilité

par 7

CD(7) = (1, 3, 2, 6, 4, 5)

La somme pondérée des chiffres de n est divisible par 7

>>>

Voir Tous les cas de sommes et produits des chiffres / Amusements avec les chiffres – Index  

 

 

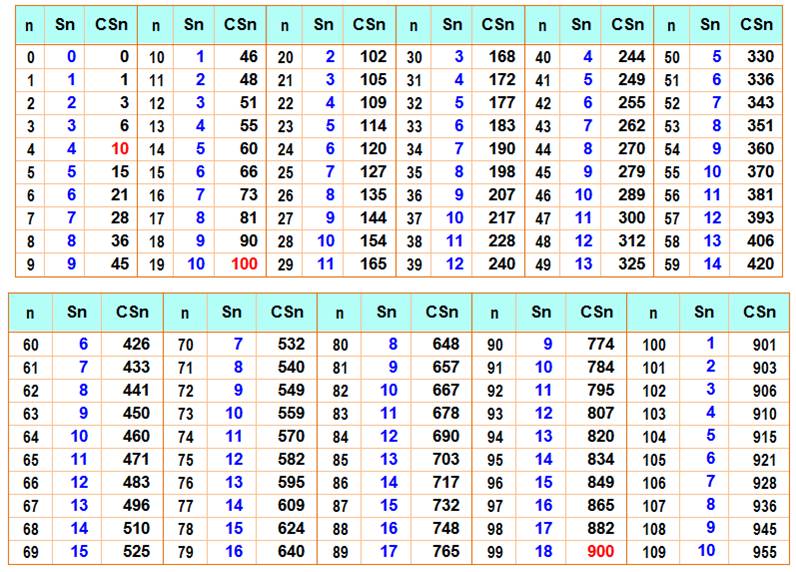
Somme des chiffres des nombres de 1 à 100

 

Tableau de n, Sn et CSn

Pour les valeurs de n, Sn est la somme de chiffres de n et CSn est le cumul

Quelques valeurs particulières en rouge.

 

Voir Tables – Index

 

 

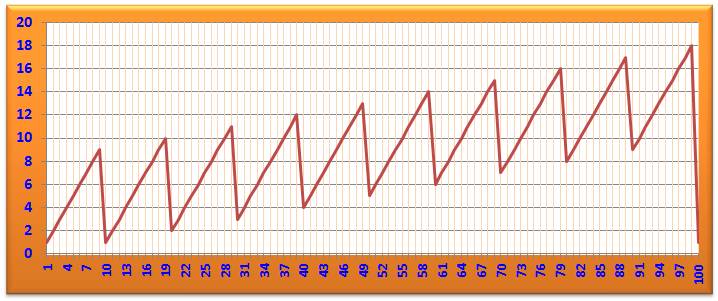
Graphe de Sn

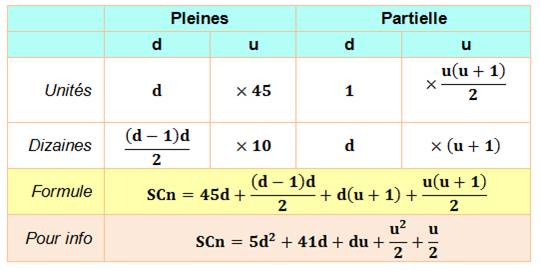
Formule de calcul de SCn (cumul)

pour n à deux chiffres

 

On note n = 10d + u

 

Pour le calcul, on distingue les dizaines pleines et la dizaine partielle

Ex: pour n = 25, il ya deux dizaines (celle en 0 et celle en 10, jusqu'à 19), et dans la dizaine partielle, il y a six nombres (20 à 25).

Jusqu'au nombre n, on compte d dizaines pleines, y compris celle avec d = 0.

Les unités "pèsent" d fois (1 + 2 +… + 9) = 45d.

Les dizaines vont en croissant de 0 à d–1. La somme de ces chiffres est (d–1) d / 2 et cela répété pour toutes les unités, soit 10 fois.

Vient ensuite la dizaine partielle qui compte u + 1 valeurs, y compris la dizaine avec 0 pour unité

Les unités "pèsent" simplement la somme des chiffres jusqu'à u, soit: u (u+1) / 2.

Les dizaines pèsent (u+1) fois la valeur de la dizaine (d).

 

Tableau montrant toutes ces formules partielles et la formule finale

 

Après cette initiation, le paragraphe suivant reprend et explique ces calculs avec un formalisme qui permettra d'établir une relation de récurrence.

 

 

Record de la somme des chiffres de 10 à 100 000

Le nombre 99 999 détient le record jusqu'à 100 000 avec une somme égale à 45 = 5 × 9

 

Le suivant est 199 999 avec la somme 46.

[10, 1], [11, 2], [12, 3], [13, 4], [14, 5], [15, 6], [16, 7], [17, 8], [18, 9], [19, 10], [29, 11], [39, 12], [49, 13], [59, 14], [69, 15], [79, 16], [89, 17], [99, 18], [199, 19], [299, 20], [399, 21], [499, 22], [599, 23], [699, 24], [799, 25], [899, 26], [999, 27], [1999, 28], [2999, 29], [3999, 30], [4999, 31], [5999, 32], [6999, 33], [7999, 34], [8999, 35], [9999, 36], [19999, 37], [29999, 38], [39999, 39], [49999, 40], [59999, 41], [69999, 42], [79999, 43], [89999, 44], [99999, 45]

Propriété

Le produit de k de 9 détient le record des plus grandes sommes des chiffres des nombres de k chiffres.  

 

 

 

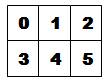
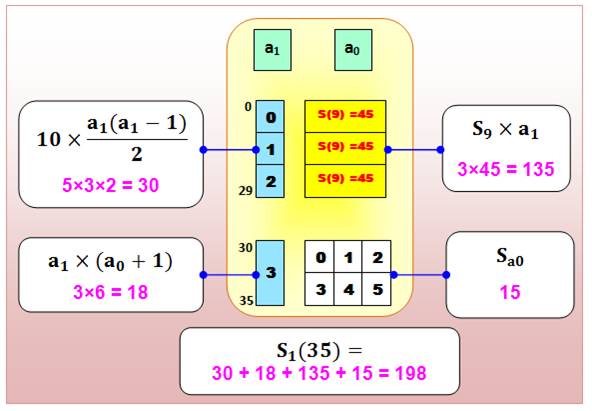
Calcul de la somme cumulée des chiffres

Un chiffre:

n = a0

 

S1(5) = ½ 5 x   6 = 15

 

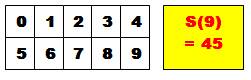
n = 99

Bloc complet des unités (0 à 9)

 

S(9) = ½ 9 x 10 = 45

 

Deux chiffres:

n = a1 a0

 

Calcul à partir de quatre blocs:

*       les dizaines entières (en haut):

*      somme des chiffres des dizaines;

*      somme des unités;

*       la dizaine partielle (en bas):

*      somme des chiffres des dizaines; et

*      somme des chiffres des unités.

Notations: a1a0 est le nombre à deux chiffres comme 35 (la notation officielle exigerait de les surligner avec une barre horizontale);

 a1 . a0 est la multiplication comme  3 x 5.

 

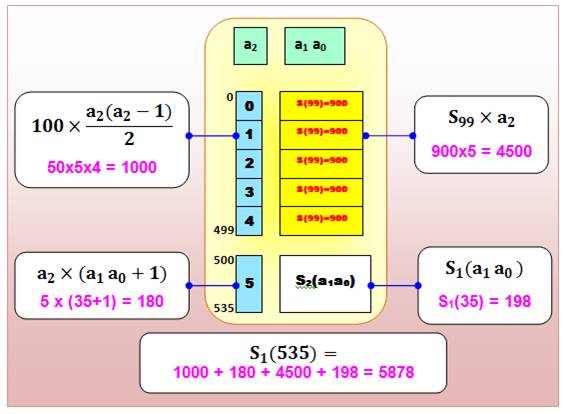
Trois chiffres:

n = a2 a1 a0

 

Calcul avec les quatre blocs qui, ici, font apparaitre la formule de récurrence possible.

On sépare les centaines pleines (en haut) mettant en évidence, en bas, la centaine partielle, composée de:

*       35 fois les nombres des centaines (à gauche), et

*       le bloc des chiffres de 0 à 35 (à droite).

 

 

Bilan

Les calculs pour les nombres à deux puis trois chiffres montrent comment calculer les quatre blocs dans le cas général à k chiffres.

Je laisse le soin au lecteur d'établir la formule générale de récurrence et sa programmation.

 

 

Records

On cherche le premier nombre n qui dépasse la somme la plus grande obtenue pour les nombres précédents. Ce sont les nombres en 9 qui ont la vedette! En effet, on a (n, Sn):

(19, 10), (29, 11) … (99, 18), (199, 19) … (999, 27), (1999, 28) …

 

 

Programmation

 

On cherche le premier nombre dont la somme des chiffres est V (exemple V = 35)

 

Programme

 

 

Commentaires

Réinitialisation avec restart.

La consigne est placée dan la mémoire V.

Un indicateur de recherche en cours est mis à 1.
Boucle de progression de 1 en 1 tant que le témoin de recherche est à 1.

Conversion de n de manière à disposer de la liste de ses chiffres.

Calcul de la somme des chiffres en S.

Si la somme est égale à la consigne, affichage (lprint) et mise à 0 du témoin de recherche.

En bleu le résultat pur la consigne  V  = 35.

Voir Programmation – Index

 

 

 

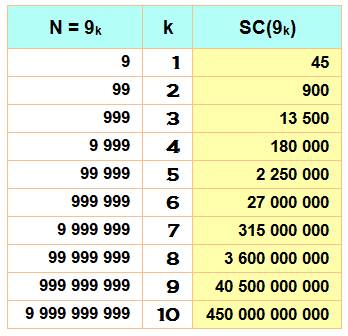
Somme des chiffres des nombres jusqu'à 99…

 

Jusqu'à 9: S(9) = 45

 

Jusqu'à 99: S(99) = 2 x 450 = 900

 

Jusqu'à 999: S(999) = 3 x 4 500 = 13 500

 

 

Jusqu'à 9k:

 

Bilan

  La somme des chiffres des nombres de 1 à     9 est égale  à       45.

  La somme des chiffres des nombres de 1 à   99 est égale  à     900.

  La somme des chiffres des nombres de 1 à 999 est égale  à 13 500.

  La somme des chiffres des nombres de 1 à 9k est égale  à 4,5k x 10k.

 

Tableau des sommes cumulées des chiffres jusqu'à n

 

 

 

 

 

 

Curiosités

 

1 + 11 + 111 + … + 11…1nfois

2 + 22 + 222 + … + 22…2nfois

3 + 33 + 333 + … + 33…3nfois

4 + 44 + 444 + … + 44…4nfois

 

= 1/81 (10n+1 – 9n – 10)

= 2/81 (10n+1 – 9n – 10)

= 1/27 (10n+1 – 9n – 10)

= 4/81 (10n+1 – 9n – 10)

 

Suite >>>

 

 

 

= 65/36

= 1,805555555 …

 

Voir Nombre 1, 8…

 

 

 

FORMULE donnant la somme de tous les chiffres des nombres de 1 à n

 

Je livre cette formule telle quelle pour ceux qui voudraient prolonger le calcul de la somme cumulée des chiffres jusqu'à n.

 

Avec

Avec

 

 Formules proposées par Medhi Aktar – Élève de seconde – Merci à lui

 

 

 

 

Nombres dont la somme des chiffres est k

haut

Légende

 

K = somme des chiffres du nombre; colonne suivante: quantité de nombres avec cette somme jusqu'à 10 000; table des nombres ayant cette somme.

Exemple: 2022 est dans la ligne  k = 6 qui comporte 84 nombres dont la somme est 6.
L'année suivante avec somme 6 sera l'année 2031.

k = 1

 5

1, 10, 100, 1000, 10000

k = 2

10

2, 11, 20, 101, 110, 200, 1001, 1010, 1100, 2000

k = 3

20

3, 12, 21, 30, 102, 111, 120, 201, 210, 300, 1002, 1011, 1020, 1101, 1110, 1200, 2001, 2010, 2100, 3000

k = 4

35

4, 13, 22, 31, 40, 103, 112, 121, 130, 202, 211, 220, 301, 310, 400, 1003, 1012, 1021, 1030, 1102, 1111, 1120, 1201, 1210, 1300, 2002, 2011, 2020, 2101, 2110, 2200, 3001, 3010, 3100, 4000

k = 5

56

5, 14, 23, 32, 41, 50, 104, 113, 122, 131, 140, 203, 212, 221, 230, 302, 311, 320, 401, 410, 500, 1004, 1013, 1022, 1031, 1040, 1103, 1112, 1121, 1130, 1202, 1211, 1220, 1301, 1310, 1400, 2003, 2012, 2021, 2030, 2102, 2111, 2120, 2201, 2210, 2300, 3002, 3011, 3020, 3101, 3110, 3200, 4001, 4010, 4100, 5000

k = 6

84

6, 15, 24, 33, 42, 51, 60, 105, 114, 123, 132, 141, 150, 204, 213, 222, 231, 240, 303, 312, 321, 330, 402, 411, 420, 501, 510, 600, 1005, 1014, 1023, 1032, 1041, 1050, 1104, 1113, 1122, 1131, 1140, 1203, 1212, 1221, 1230, 1302, 1311, 1320, 1401, 1410, 1500, 2004, 2013, 2022, 2031, 2040, 2103, 2112, 2121, 2130, 2202, 2211, 2220, 2301, 2310, 2400, 3003, 3012, 3021, 3030, 3102, 3111, 3120, 3201, 3210, 3300, 4002, 4011, 4020, 4101, 4110, 4200, 5001, 5010, 5100, 6000

k = 7

120

7, 16, 25, 34, 43, 52, 61, 70, 106, 115, 124, 133, 142, 151, 160, 205, 214, 223, 232, 241, 250, 304, 313, 322, 331, 340, 403, 412, 421, 430, 502, 511, 520, 601, 610, 700, 1006, 1015, 1024, 1033, 1042, 1051, 1060, 1105, 1114, 1123, 1132, 1141, 1150, 1204, 1213, 1222, 1231, 1240, 1303, 1312, 1321, 1330, 1402, 1411, 1420, 1501, 1510, 1600, 2005, 2014, 2023, 2032, 2041, 2050, 2104, 2113, 2122, 2131, 2140, 2203, 2212, 2221, 2230, 2302, 2311, 2320, 2401, 2410, 2500, 3004, 3013, 3022, 3031, 3040, 3103, 3112, 3121, 3130, 3202, 3211, 3220, 3301, 3310, 3400, 4003, 4012, 4021, 4030, 4102, 4111, 4120, 4201, 4210, 4300, 5002, 5011, 5020, 5101, 5110, 5200, 6001, 6010, 6100, 7000

k = 8

165

8, 17, 26, 35, 44, 53, 62, 71, 80, 107, 116, 125, 134, 143, 152, 161, 170, 206, 215, 224, 233, 242, 251, 260, 305, 314, 323, 332, 341, 350, 404, 413, 422, 431, 440, 503, 512, 521, 530, 602, 611, 620, 701, 710, 800, 1007, 1016, 1025, 1034, 1043, 1052, 1061, 1070, 1106, 1115, 1124, 1133, 1142, 1151, 1160, 1205, 1214, 1223, 1232, 1241, 1250, 1304, 1313, 1322, 1331, 1340, 1403, 1412, 1421, 1430, 1502, 1511, 1520, 1601, 1610, 1700, 2006, 2015, 2024, 2033, 2042, 2051, 2060, 2105, 2114, 2123, 2132, 2141, 2150, 2204, 2213, 2222, 2231, 2240, 2303, 2312, 2321, 2330, 2402, 2411, 2420, 2501, 2510, 2600, 3005, 3014, 3023, 3032, 3041, 3050, 3104, 3113, 3122, 3131, 3140, 3203, 3212, 3221, 3230, 3302, 3311, 3320, 3401, 3410, 3500, 4004, 4013, 4022, 4031, 4040, 4103, 4112, 4121, 4130, 4202, 4211, 4220, 4301, 4310, 4400, 5003, 5012, 5021, 5030, 5102, 5111, 5120, 5201, 5210, 5300, 6002, 6011, 6020, 6101, 6110, 6200, 7001, 7010, 7100, 8000

k = 9

220

9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 108, 117, 126, 135, 144, 153, 162, 171, 180, 207, 216, 225, 234, 243, 252, 261, 270, 306, 315, 324, 333, 342, 351, 360, 405, 414, 423, 432, 441, 450, 504, 513, 522, 531, 540, 603, 612, 621, 630, 702, 711, 720, 801, 810, 900, 1008, 1017, 1026, 1035, 1044, 1053, 1062, 1071, 1080, 1107, 1116, 1125, 1134, 1143, 1152, 1161, 1170, 1206, 1215, 1224, 1233, 1242, 1251, 1260, 1305, 1314, 1323, 1332, 1341, 1350, 1404, 1413, 1422, 1431, 1440, 1503, 1512, 1521, 1530, 1602, 1611, 1620, 1701, 1710, 1800, 2007, 2016, 2025, 2034, 2043, 2052, 2061, 2070, 2106, 2115, 2124, 2133, 2142, 2151, 2160, 2205, 2214, 2223, 2232, 2241, 2250, 2304, 2313, 2322, 2331, 2340, 2403, 2412, 2421, 2430, 2502, 2511, 2520, 2601, 2610, 2700, 3006, 3015, 3024, 3033, 3042, 3051, 3060, 3105, 3114, 3123, 3132, 3141, 3150, 3204, 3213, 3222, 3231, 3240, 3303, 3312, 3321, 3330, 3402, 3411, 3420, 3501, 3510, 3600, 4005, 4014, 4023, 4032, 4041, 4050, 4104, 4113, 4122, 4131, 4140, 4203, 4212, 4221, 4230, 4302, 4311, 4320, 4401, 4410, 4500, 5004, 5013, 5022, 5031, 5040, 5103, 5112, 5121, 5130, 5202, 5211, 5220, 5301, 5310, 5400, 6003, 6012, 6021, 6030, 6102, 6111, 6120, 6201, 6210, 6300, 7002, 7011, 7020, 7101, 7110, 7200, 8001, 8010, 8100, 9000

Stat.

 

Quantité de nombres avec somme k jusqu'à 10 000
511, 10, 20, 35, 56, 84, 120, 165, 220, 28210,
348, 415, 480, 540, 592, 633, 660, 670, 660, 63320,
592, 540, 480, 415, 348, 282, 220, 165, 120, 8430,
56, 35, 20, 10, 4, 1, 037.
La somme final (unique) étant 9 + 9 + 9 + 9 = 36

 

Voir Racine numérique des nombres

 

 

 

 

 

Suite

*      Chiffres – Index

*      Table et calcul de la somme des chiffres de 0 à 1 000 000

*      Table des nombres + somme des chiffres

*      Somme des entiers

*      Racine numérique (de la preuve par neuf)

*      Addition – Glossaire

Voir

*      Carrés

*      Cubes

*      Factorielles et somme des entiers

*      Fonctions arithmétiques – Liste

*      Isopérimètre

*      Nombres consécutifs – Index

*      Nombres géométriques

*      Théorèmes

*      Somme-Produit des chiffres – Index

Diconombre

*      Nombre 45

*      Nombre 900

*      Nombre 13 500

*      Nombre 180 000

Sites

*      OEIS A007953 – Digital sum of n (digsum)

*      OEIS A037123 – a(n) = a(n-1) + Sum of digits of n

*      OEIS A052220 - Numbers whose sum of digits is 6

*      OEIS A217747 - Numbers whose digits sum to a perfect number

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomChiff.htm