Nombre égal à la moyenne de ses chiffres

Édition du: 29/06/2025

INDEX Chiffres Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Sommes de nombres	CHIFFRES
	Chiffres	Chiffres en barres	Chiffres et doigts
	Chiffres différents	S. de chiffres	Moyenne des chiffres
	Programmes et chiffres		Fréquence (Benford)

Faites un double-clic pour un retour en haut de page

Nombres égaux à la moyenne

de la somme de ses chiffres

Ces nombres sont peu nombreux !

Occasion d'un exercice de programmation Python.

Sommaire de cette page

>>> Nombres EM0S0CH

>>> Programmation Python

Débutants

Chiffres et Nombres

Glossaire

Chiffres

Nombres EM0S0CH Égal à la moyenne de la somme des chiffres		haut
Définition Nombre décimal comportant des zéros à droite, tel que la somme des chiffres, divisée par la quantité de chiffres, la moyenne, est égale au nombre. Commentaire Les nombres à un seul chiffre sont des exemples triviaux: 5 à pour moyenne 5. Notez que les autres nombres entiers produisent des sommes inférieures au nombre. Ex: 99 => 9 + 9 = 18 et 18 < 99. Seuls des nombres décimaux sont susceptibles de satisfaire l'exigence de l'égalité. Qui plus est, il est nécessaire de leur adjoindre des zéros obligatoires à droite (trailing zeros).	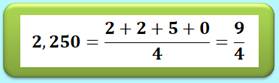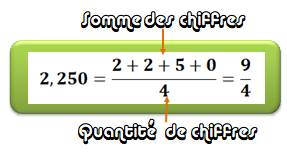Exemple de nombre EMOSOH Notez que le zéro final est nécessaire pour calculer la moyenne indiquée.
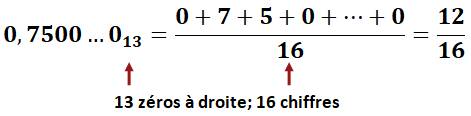
Exemple avec nombreux 0 à droite
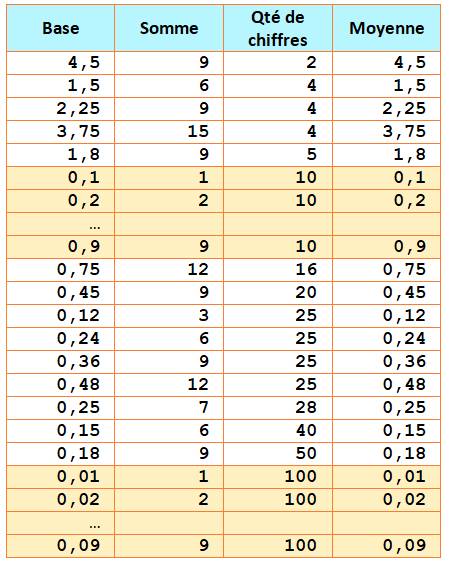
Liste En coloré ocre, des valeurs triviales. Voir DicoNombre (accès à tous les nombres du dictionnaire), dont: Nombre 0,75 Nombre 1,5 Nombre 1,8 Nombre 2,25 Nombre 3,75 Nombre 4,5

Programmation Python avec commentaires			haut
But Recherche systématique des nombres égaux la moyenne de ses chiffres. Soit: édition des valeurs figurant dans le tableau ci-dessus. Pistes La principale difficulté est liée au fait que les zéros de droite sont obligatoires. Or, les programmes mathématiques les ignorent systématiquement: nous allons considérer les chiffres comme des caractères en les convertissant avec str (string). Avantage également pour effectuer des comparaisons rigoureuses en évitant les effets d'arrondis. Le traitement de grands nombres nécessite d'augmenter la quantité de décimales requise. Ici: 100 et cela avec appel au module décimal. Notez que l'appel n'est pas banal ! Notez aussi que, les nombres sont stockés en binaire et sans la précision voulue, le logiciel extrapole n'importe quoi. Alors que vous attendiez: 2,20000000000 vous aurez peut-être 2,20000001423, faussant évidemment les comparaisons. La suite est expliquée dans les commentaires au sein du programme.
Programme Python from decimal import Decimal, getcontext getcontext().prec = 100 def Moy(n,k): Tx = f"{n:.{k}f}" Ch = [int(c) for c in Tx if c.isdigit()] return sum(Ch) / len(Ch) for k in range (1,100): for i in range (1,100000): n = Decimal(str(i/100)) m = Moy(n,k) if m == i/100 : som = sum([int(c) for c in f"{n:.{k}f}" if c.isdigit()]) print(k,i,n,"et",som, som/(k+1)) Programme Python avec commentaires # On importe le module 'decimal' pour effectuer des calculs avec une précision contrôlée from decimal import Decimal, getcontext # On définit ici la précision globale des calculs : 100 chiffres significatifs getcontext().prec = 100 # ─────────────── # FONCTION Moy() # ─────────────── def Moy(n, k): """ Calcule la moyenne des chiffres significatifs (y compris les zéros) d'un nombre décimal 'n', comportant 'k' décimales. """ # On convertit le nombre n en chaîne de caractères avec exactement k chiffres après la virgule Tx = f"{n:.{k}f}" # On extrait uniquement les chiffres (on ignore le point ou la virgule) et les convertit en entiers. isdigit() détecte la présence d'un chiffre dans une chaine de caractères (famille des string methods). Ch = [int(c) for c in Tx if c.isdigit()] # On retourne la moyenne de ces chiffres (somme divisée par leur quantité) return sum(Ch) / len(Ch) # ───────────────────────────────────── # BOUCLE PRINCIPALE POUR EXPLORATION # ───────────────────────────────────── # k = nombre de décimales imposées (de 1 à 99) for k in range(1,100): # i représente un nombre entier de 1 à 99 999 for i in range(1, 100000): # On transforme i en centième : 1 → 0.01, 250 → 2.50, etc. # On passe par str() pour conserver la précision du résultat décimal n = Decimal(str(i / 100)) # On calcule la moyenne des chiffres du nombre n affiché avec k décimales m = Moy(n, k) # Si la moyenne est égale exactement à la valeur d’origine... if m == i / 100: # On recalcule la somme des chiffres affichés som = sum([int(c) for c in f"{n:.{k}f}" if c.isdigit()]) # On affiche : # - k : le nombre de décimales utilisées # - i : le numéro "brut" avant division par 100 # - n : le nombre de base # - som : la somme des chiffres significatifs # - som / (k + 1) : la moyenne retrouvée pour vérification print(k, i, n, "et", som, som / (k + 1))
Résultats 1 450 4.5 et 9 4.5 3 150 1.5 et 6 1.5 3 225 2.25 et 9 2.25 3 375 3.75 et 15 3.75 4 180 1.8 et 9 1.8 9 10 0.1 et 1 0.1 9 20 0.2 et 2 0.2 9 30 0.3 et 3 0.3 9 40 0.4 et 4 0.4 9 50 0.5 et 5 0.5	9 60 0.6 et 6 0.6 9 70 0.7 et 7 0.7 9 80 0.8 et 8 0.8 9 90 0.9 et 9 0.9 15 75 0.75 et 12 0.75 19 45 0.45 et 9 0.45 24 12 0.12 et 3 0.12 24 24 0.24 et 6 0.24 24 36 0.36 et 9 0.36 24 48 0.48 et 12 0.48 27 25 0.25 et 7 0.25	39 15 0.15 et 6 0.15 49 18 0.18 et 9 0.18 99 1 0.01 et 1 0.01 99 2 0.02 et 2 0.02 99 3 0.03 et 3 0.03 99 4 0.04 et 4 0.04 99 5 0.05 et 5 0.05 99 6 0.06 et 6 0.06 99 7 0.07 et 7 0.07 99 8 0.08 et 8 0.08 99 9 0.09 et 9 0.09

Voir Programmation – Index / Programmes Python – Index

Haut de page (ou double-clic)

Retour	Somme des chiffres
Suite	Chiffres – Index Table et calcul de la somme des chiffres de 0 à 1 000 000 Table des nombres + somme des chiffres Somme des entiers Racine numérique (de la preuve par neuf) Addition – Glossaire
Voir	Carrés Cubes Factorielles et somme des entiers Fonctions arithmétiques – Liste Isopérimètre Nombres consécutifs – Index Nombres géométriques Théorèmes Somme-Produit des chiffres – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/MoyChiff.htm