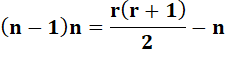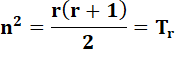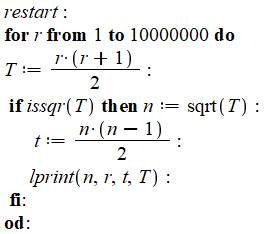|
Édition du: 13/12/2023 |
|
INDEX Nombres (Classification) |
Types de Nombres – Motifs |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Suites équilibrées
Égalité entre
deux sommes de nombres consécutifs. Recherche des nombres triangulaires
carrés. |
||
|
|
Sommaire de cette page >>> Nombres de suites équilibrées >>> Nombres médians de suites équilibrées >>> Propriétés et historique >>> Programme Maple >>> Cas où n fait partie de la première suite |
Débutants Glossaire |
|
Définition Un tel nombre n est au milieu de deux sommes identiques de nombres
consécutifs.
|
1 + 2 + … + (n – 1)
= (n + 1) + (n + 2) + … r |
|
|
Nombre triangulaire
|
|
|
|
Formulation La somme des nombres de 1 à k s'écrit: k (k + 1)
/ 2. Conclusion: le nombre n au carré est égal au
nombre triangulaire d'ordre r. |
|
|
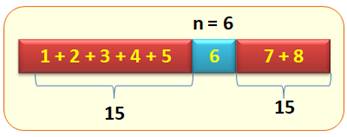
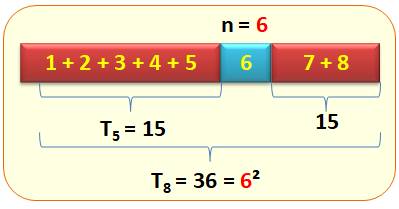
Illustration avec n = 6
|
Calcul On cherche les nombres triangulaires carrés. On vérifie que, par exemple pour n = 35:
|
|
|
|
Liste Ces nombres au carré sont triangulaires. Ils sont situés au centre de
deux suites de nombres consécutifs de même somme. |
0, 1, 6, 35, 204, 1189, 6930, 40391, 235416, 1372105,
7997214, 46611179, 271669860, 1583407981, 9228778026, 53789260175,
313506783024, 1827251437969, 10650001844790, 62072759630771, 361786555939836,
2108646576008245, 12290092900109634, 71631910824649559, … |
|
|
Propriétés |
Le nombre n est un "médian" de la suite 1 + 2 + … + r Ces nombres au carré sont des nombres triangulaires. Les nombres 8n² + 1 sont des carrés. Ex: 8 × 35² + 1 = 9801
= 99². Ces nombres sont solutions de l'équation diophantienne x² – 8y² = 1. Valeur du produit xy où (x, y)
satisfait x² – 2y² = +1 ou -1. Formule de récurrence: Un = 6Un-1 – Un-2
avec U0 = 0 et U1 = 1. |
|
|
Historique |
L'encyclopédie des nombres répertorie ces nombres comme racine carrée
entière de nombres triangulaires. Behera et Panda (1999) appellent ces nombres des balancing numbers et
le nombre n lui-même un balancer. Sujet abordé par Ramanujan sous la forme d'une énigme à propos de la somme
des numéros des maisons avant et après une certaine maison médiane. Voir aussi, l'énigme de la maison du
maire. |
|
|
|
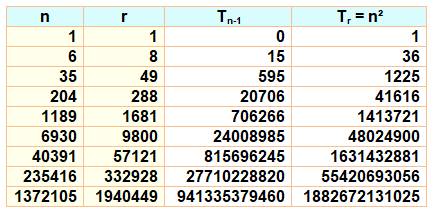
But Éditer le tableau vu ci-dessus. avec Maple. Commentaires Exploration des nombres triangulaires T de rang
r. Test si ce nombre est carré avec issqr (is square). Impression de n, la racine carrée du nombre
triangulaire, de r, de t = Tn-1
et de T = Tr |
|
Voir Programmation – Index
|
Définition
|
1 + 2 + … + (n)
= (n + 1) + (n + 2) + … r ex: 1 + 2 + … + 14 = 15 + 16 + … + 20 = 105 ex: 1 + 2 + … + 84 = 85 + 86 + … + 119 = 3570 ex: 1 + 2 + … + 492 = 493 + … + 696 = 121 278 ex: 1 + 2 + … + 2870 = 2871 + … + 4059 = 4 119
885 |
|
|
Propriété |
Nombre tel que son double est également triangulaire Ex: T14 = 105 et T20 = 210 |
|
|
Liste Indice des nombre triangulaires qui sont la moitié d'un autre
triangulaire. |
0, 2, 14, 84, 492, 2870, 16730, 97512,
568344, 3312554, 19306982, 112529340, 655869060, 3822685022, 22280241074,
129858761424, 756872327472, 4411375203410, 25711378892990, 149856898154532,
873430010034204, … |
|
Voir Énigme
des numéros des maisons
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |