NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/07/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	GÉOMÉTRIQUES			Glossaire Carrés magiques
INDEX Carrés magiques	Général	Polygones	Étoiles	Cubes
	Pentagones	Hexagones	Couronnes
		Sommaire de cette page >>> Hexagone magique d'ordre 3 >>> Énigme >>> Solution

Devinette des six nombres

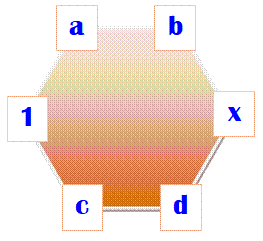
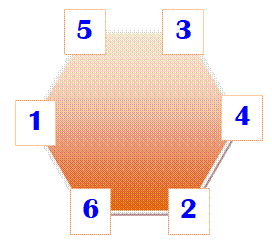
Placez les nombres de 1 à 6 dans cet hexagone de sorte que la somme de deux nombres consécutifs soit toujours 6, 7 ou 8.

Énigme de niveau école primaire

Solution

Hexagone magique d'ordre 3
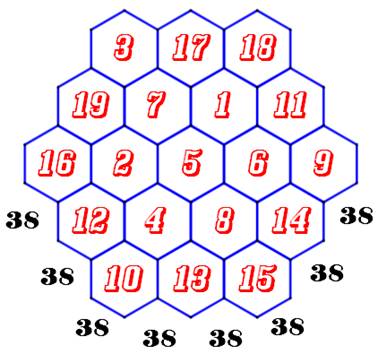
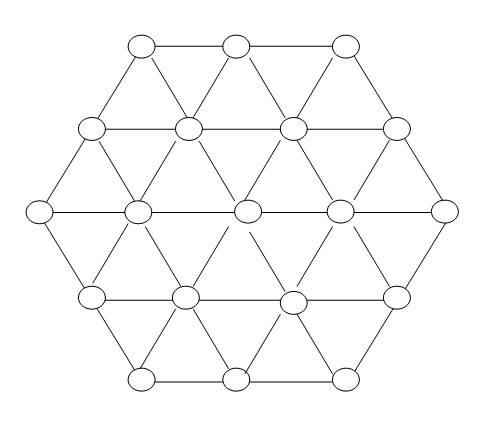
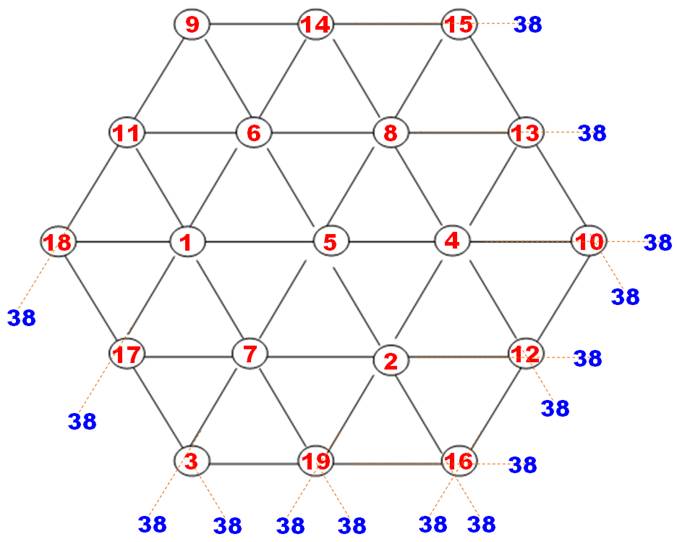
Somme magique de l'hexagone magique d'ordre 3: 38. Nombres utilisés de 1 à 19 Tous les alignements de trois ou quatre nombres forment la somme magique. Exemple 10 + 13 + 15 = 12 + 4 + 8 + 14 = … 3 + 19 + 16 = 17 + 7 + 2 + 12 = … Historique 1887 – Ernst von Haselberg pour la référence connue la plus ancienne. 1964 – Charles Trigg: hors symétries, cet hexagone magique d'ordre 3 est unique.

Énigme

Remplir cet hexagone avec les nombres de 1 à 19 tout en ayant la même somme sur chaque des lignes. On note que tous les nombres sont distribués sur cinq lignes dont chaque somme est S. Or la somme des nombres de 1 à 19 est égale à: 19 x 20 / 2 = 190. La somme magique est donc égale à: S = 190/ 5 = 38. Existe-t-il une méthode simple pour résoudre ce puzzle? J'en doute! Il existe 30 possibilités (plus leurs permutations) de faire 38 en trois nombres différents. Il y en a 147 pour 4 et 238 pour 5. Ce qui montre que l'exploration n'est pas simple. Même par programmation la rédaction du programme est longue et fastidieuse.

Solution
Voici l'unique solution: Doublement unique: seule configuration possible avec cet hexagone avec trois cases par côtés (on dit que l'hexagone est d'ordre n = 3) seule solution possible quelle que soit la quantité n de cases par côtés.

Devinette – Solution

À partir du 1 déjà placé, pour atteindre 6, 7 ou 8, on a le choix entre 5 et 6 seulement. L'un va en haut du 5, l'autre en bas. Nombres qui restent: 2, 3 et 4. Après le 6, seul le 2 convient pour faire la somme 8; en effet, 3 et 4 sont trop grands. Avec le 3 et le 4 qui restent, seul le 4 convient après le 2.

Retour / Autres énigmes / Brève n°410

Suite	Hexagones Polygones magiques Carrés magiques et jeux Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie – Index Jeux – Index Jeux de chiffres Nombres magiques – Index Pannumérique Rubriques débutants – Index Sudoku
Aussi	Polygone Hexagone
Sites	Liens vers les sites carrés magiques Hexagone magique – Wikipédia Magic hexagon – Mathworld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMgeomHe.htm