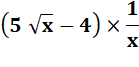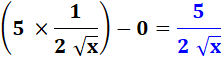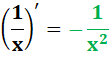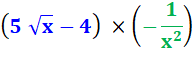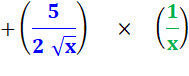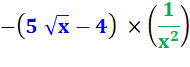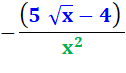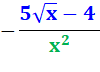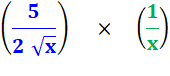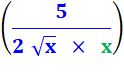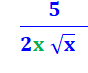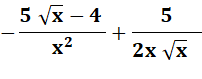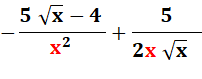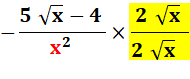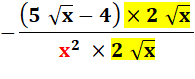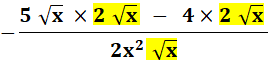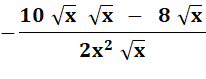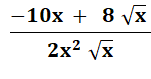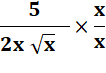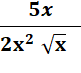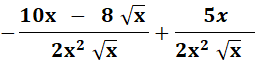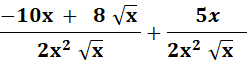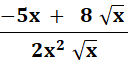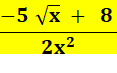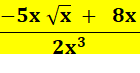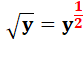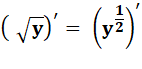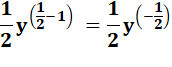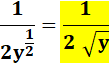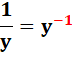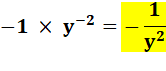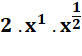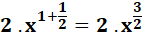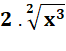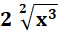|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
DÉRIVÉES – Exemple avec racines Exemples développés à fond
pour resynchroniser les personnes qui auraient un peu décroché. |
|
|
|||
|
|
f = |
|
|
|
On pourrait également la voir sous la forme d'une fraction: u / v'
avec v' = x. |
f = |
|
|
|
u = |
|
||
|
v = |
|
||
|
|
f' =(u . v)' = f' = (uv)' = |
u . v' + u' . v uv' + u'v |
|
|
u' = |
|
|
|
v' = |
|
|
|
f' = uv' + u'v = |
|
|
|
A1 = |
|
|
|
A2 = |
|
|
|
|
|
|
|
f'
= (uv)' = |
|
|
|
A1
= |
|
|
|
A1
= |
|
|
|
A2
= |
|
|
|
f'
=(uv)'= A1
+ A2 = |
|
|
|
f'
= |
|
|
|
f'
= |
|
|
|
||
|
|
Instructions Maple Notez que deux étapes finales sont nécessaires pour
obtenir une fraction simple sans radicaux au dénominateur. Entrée de l'expression. Demande du calcul de la dérivée (différentiel)
par rapport à x. Simplification des radicaux, spécialement au
dénominateur. Élimination des radicaux au dénominateur. |
|
Voir Programmation
|
|
|||
|
|
f = f' = |
|
|
|
|
a = |
|
|
|
|
a' = |
|
|
|
|
a' = |
|
|
|
|
a' = |
|
|
Retour à l'exercice
Voir Dérivées usuelles
/ Exemple de calcul
|
|
|||
|
|
a = |
|
|
|
|
a' = |
|
|
|
|
a' = |
|
|
Retour à l'exercice
À retenir
|
Une
puissance négative y-a
est
l'inverse de la puissance : 1 / ya
. Une
puissance fractionnaire y1/a
est
une racine : |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Retour à l'exercice
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
http://villemin.gerard.free.fr/aMaths/Analyse/DerivInt/DerivEx1.htm |
![]()