NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/07/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	CHIFFRES & LETTRES
Débutants Cryptarithme	PUZZLES ARITHMÉTIQUES					Glossaire Général
INDEX Puzzles Jeux de nombres Jeux numériques	Additions		Soustractions	Amour+haine	Libres (à trous)
	Pastilles		Multiplications	Valet	Dix² - Six²
	One four nine		Divisions	One Two	Twenty
	Notes de musique		Triplets pannum.	Cats and dogs
		Sommaire de cette page >>> Addition à résoudre >>> Étape 1 – Estimation de la somme maximale >>> Retenues >>> Étape 2 – Valeur de F et de I >>> Étape 3 – Valeur de 0, T et de G >>> Étape 4 – Essais avec 0 = 5 et T = 6 >>> Étape 4bis – Essais avec 0 = 6 et T = 8 >>> SOLUTION

PUZZLES ARITHMÉTIQUES

Cryptarithmes – Cryptogrammes

Exemple de recherche de solution.

Nous allons décortiquer toutes les étapes de déduction pour arriver à la solution.

Devinette

Pour se lancer, un cryptarithme à solutions multiples.

Il y a huit lettres différentes, donc huit chiffres différents; certains sont doublés (en rouge).

Solution

ADDITION à résoudre
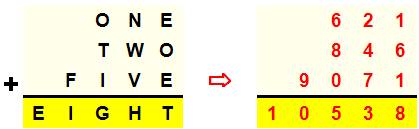
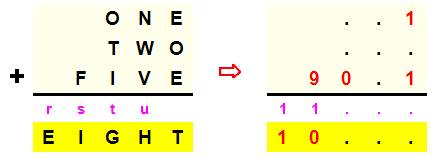
Problème & sa solution Il existe Six solutions avec permutations des 2, 4 et 7. Rappel: chiffres en anglais 1 ONE 2 TWO 5 FIVE 8 EIGHT Notez bien que l'égalité en anglais est correcte: 1 + 2 + 5 = 8. Voir Nombre 10 538/ Anglais

Résolution pas à pas

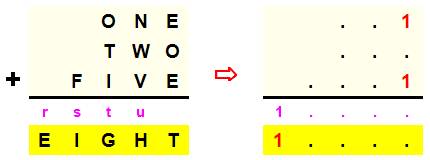
Étape 1 – Estimation de la somme maximale

L'idée est que: EIGHT possède un chiffre de plus que FIVE; E n'est pas 0 (sinon EIGHT serait IGHT); E est manifestement une retenue: 1 ou 2. Essayons d'apprécier sa valeur: on place les plus grands chiffres le plus à gauche possible pour faire la plus grosse somme. On ne s'embarrasse pas, dans un premier temps, de la question des lettres identiques. Voici la disposition des chiffres, tous différent, qui donnerait la plus grande somme (11 223)

RETENUES
Nous avons admis que la retenue est égale à 1, est-ce si évident? La somme maximale pour une addition de deux termes est celle de 9 + 9 = 18; retenue 1. Avec trois termes: 9 + 9 + 9 = 27: retenue 2. Etc. Pour une somme de n chiffres, la retenue maximale est égale à n. Configuration particulière (celle à gauche de notre énigme). Ce qui justifie que E = 1.

Étape 2 – Valeur de F et de I
On sait que =>	E = r = 1
La somme F + s doit produire la retenue r = 1.	F + s = 1
On a vu que dans cette configuration la retenue s ne peut être que 1 ou 2.	s = 1 s = 2
Il faut que F fasse le maximum pour hisser la somme F + s à 10 ou plus. Se souvenir que F est un chiffre (donc <10).	F = 8 et F+1 = 9 non F = 8 et F+2 = 10 BON F = 9 et F+1 = 10 BON F = 9 et F+2 = 11 BON F = 10 non
Possibilités pour F et I.	F = 8 et I = 1 F = 9 et I = 0
Or le chiffre 1 a déjà été attribué à E.	I = 0 et F = 9

Étape 3 – Valeur de 0, T et de G
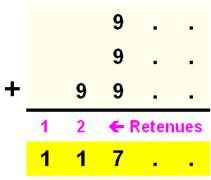
Écrivons la somme suivante => Avec sa retenue connue s = 1.	O + T + t = 10 + G
C'est une somme de deux chiffes (O et T). La retenue maximale est 1.	t = 0 t = 1
Une autre somme va nous aider.	1 + O + 1 = T T = O + 2
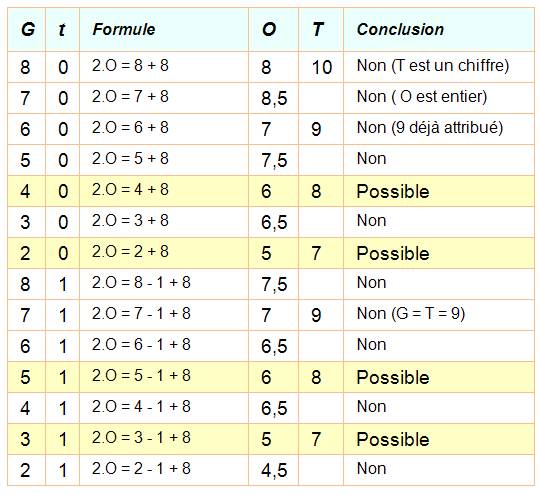
Reprenons la première équation. Et évaluons G (qui est un chiffre).	O + T + t = 10 + G O + O + 2 + t = 10 + G 2 . O = G – t + 8
Le chiffre 9 étant déjà attribué, la valeur maximale de G est 8.	Gmax = 8
Voyons les cas possibles pour G et t et calculons O et T.	2 . O = G – t + 8 T = O + 2
Soit quatre cas possibles avec O et T qui valent (5, 7) ou (6,8).

Étape 4 – Essais avec 0 = 5 et T = 6
Premier cas:	G = 2 et t = 0
Chiffres qui ne sont pas encore attribués:	3, 4, 6, 8
Ces 4 valeurs sont celles à mettre dans la colonne libre.	N + W + V = H
Avec ces valeurs, la somme H n'est jamais inférieure à 10.	3 + 4 + 6 = 13 => NON
Deuxième cas:	G = 3 et t = 1
Ces 4 valeurs sont celles à mettre dans la colonne libre + retenue.	N + W + V + 1 = H
Chiffres qui ne sont pas encore attribués.	2, 4, 6, 8
Avec ces valeurs la somme H n'est jamais inférieure à 10.	2 + 4 + 6 + 1 = 13 => NON
Ces deux cas sont à :	Rejeter

Étape 4bis – Essais avec 0 = 6 et T = 8
Premier cas.	G = 4 et t = 0
Chiffres qui ne sont pas encore attribués.	2, 3, 5, 7
Ces 4 valeurs sont celles à mettre dans la colonne libre.	N + W + V = H
Avec ces valeurs, la somme H inférieure à 10 donne 9 et non le 7 restant (et 9 et déjà attribué).	2 + 3 + 5 = 9 => NON
Deuxième cas.	G = 5 et t = 1
Ces 4 valeurs sont celles à mettre dans la colonne libre + retenue.	N + W + V + 1 = H
Chiffres qui ne sont pas encore attribués.	2, 3, 4, 7
Avec ces valeurs la somme doit donner une retenue (>10), et H doit être le chiffre restant.	2 + 3 + 4 = 9 Non 2 + 3 + 7 = 12 Non 2 + 4 + 7 = 13 OUI, Bingo 3 + 4 + 7 = 14 Non
Seule possibilité =>	G = 5 H = 3 N, W, V = {2, 4, 7}

SOLUTION
Notez que les lettres N, W et V de l'avant-dernière colonne valent (2, 4, 7) dans l'ordre que l'on veut. Soit 6 solutions possibles.

Devinette – Solution

Résoudre ce cryptarithme Solutions Il y en a 44 en admettant le 0 interne, et 28 sans présence de 0.
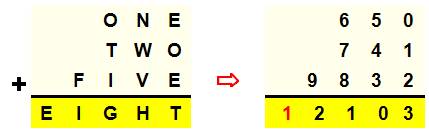
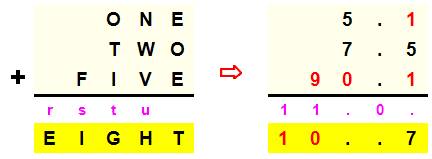
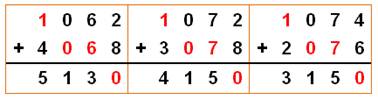
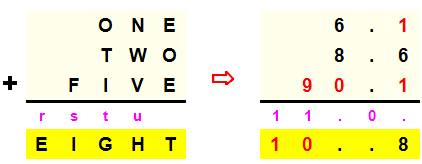
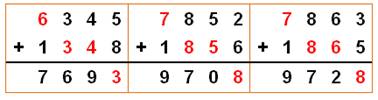
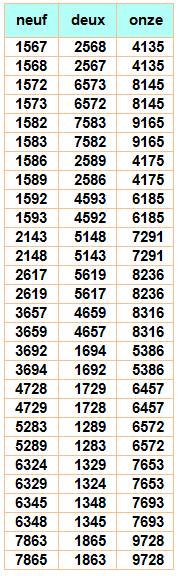
Les trois solutions les plus petites Les unités peuvent être échangées. Ex: 2 et 8 pour 8 et 2 dans le premier. Les trois plus grandes dont deux sans 0 interne:	Les 28 solutions sans 0:

Retour

Suite	Autre exemple avec twenty Autres pages
Voir	Alphabet parlant Anagramme de chiffres Jeux – Index
Diconombre	Nombre 10 538
Livre	Pour le plaisir de se casser la tête de Louis Thépault – Il comporte de nombreux cas avec leur résolution – Passionnant!
Sites	Voir Liste
Cette page	http://villemin.gerard.free.fr/Puzzle/lettadd1.htm