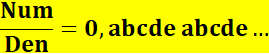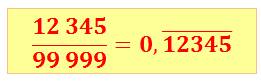NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 23/11/2021

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique     Brèves de Maths

      

CHIFFRES & LETTRES

 

Débutants

Cryptarithme

PUZZLES

ARITHMÉTIQUES

 

Glossaire

Général

 

 

INDEX

PUZZLES

 

Additions

Soustractions

Amour+haine

Libres

Pastilles

Multiplications

Valet

Dix² – Six²

One four nine

Divisions

One Two

Twenty

Fractions

 

Sommaire de cette page

>>> Fraction – Amour

>>> Fraction – Vallée

>>> Division N°1

>>> Division N°2

 

 

 

PUZZLES ARITHMÉTIQUES

 Cryptarithmes ou cryptogrammes

avec des fractions et des divisions

 

Pour se lancer, voir FRACTIONS = 248615397  (niveau primaire)

 

 

Exemple à solution unique

La barre sur vallée indique que ces décimales se répètent sans fin

4715 / 27027 = 0,174455 174455 …

 

 

Fraction – Amour

Cryptarithme

 

Remplacer les lettres par des chiffres non-nuls.

Si possible tous les chiffres de la fraction et de la période seront différents.

 

 

abcde peut parfois être agrémenté en le baptisant AMOUR ou DÉSIR ou ...

 

 

Un des solutions

 

Pour l’explication, partons d'une solution pour mieux comprendre comment y arriver.

Codage

 

A

M

O

U

R

N

D

1

2

5

4

6

34

271

 

Création d’une fraction

 

Un million de fois S moins S donne un nombre entier multiple de 999 999.

 

Voir Nombres cycliques

                S =           0,12546 12546

100 000 S = 12546,12546 ...

   99 999 S = 12546

Den est un diviseur de 99 9999

99 999 = k x Den

99 999 = 3 x 3 x 41 x 271

Diviseurs (3, 9, 41, 123, 271, 369,

                      813, 2439, 11 111)

Essais (au hasard) avec Num = 1 et Den = 271

Essais avec Num = 2, 3, … 34

 

Unicité de solution ? NON

Il y en a 15 120 avec aucun 0

                30 240 avec des 0

 

Numérateur à un chiffre, le 0 est admis – 8 solutions.

Aucun à un chiffre le zéro état nt exclu.

Avec deux chiffres au numérateur et aucun 0 – 12 solutions.

 

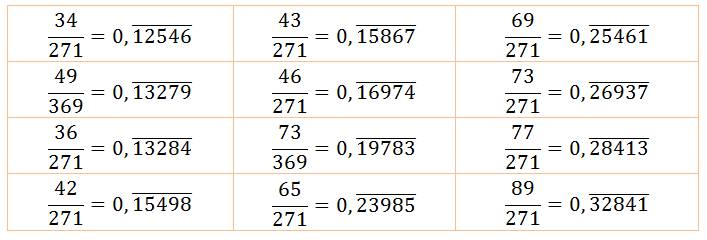
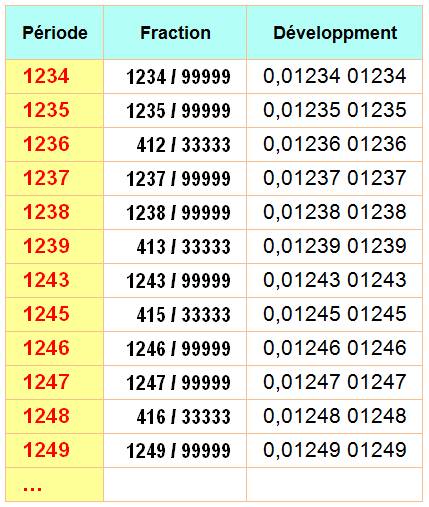
Les douze premières valeurs (en admettant les 0)

 

Chiffres différents

La seule solution avec tous les chiffres différents (hormis le 0, débutant le développement décima) =>

Pas facile de trouver cette valeur sans programmation !

 

Solution triviale

Fraction valable quelle que soit les chiffres au numérateur pourvu que la quantité de 9 au dénominateur soit égale à celle du numérateur: Ex: 456/999 = 0,456 456 …

 

Voir Amour + haine / Pannumérique

 

 

Fraction –Vallée

 

Remplacer les lettres par des chiffres.

 

Note: une lettre peut très bien valoir 0, malgré la présence du "0,"  débutant un nombre décimal.

 

 

Solution

 

Pour l’explication, partons de la solution pour mieux comprendre comment y arriver.

Codage

 

V

A

L

E

M

G

1

7

4

5

2

0

 

Création d’une fraction

 

Un million de fois S moins S donne un nombre entier multiple de 999 999.

                    S =             0,174455 174455

1 000 000 S = 174455,174455 ,0,0,0

   999 999 S = 174 455

 

 

Exploitation de la fraction

 

En introduisant le facteur de proportionnalité k.

Dit-autrement, la fraction VALLEE / 999999 peut être simplifiée en LAVE / MAGMA.

 

 

999 999 = k x MAGMA

VALLEE  = k x LAVE

 

 

Résolution de 999 999

Une exploration par tableur des divisions possibles de 999  999  donnant un nombre à six chiffres ( de MAGMA) et avec le motif MAGMA permet de trouver  eux possibilités:

 

999 999 = 37 x 27 027 et

999 999 = 27 x 37 037

Avec 27 027

Nouvelle égalité:

 

Dont on déduit l’unité E = 5.

L7VE x 37 = V7LLEE

 

L7V5 x 37 = V7LL55

Essais avec les dizaines:

V5 x 37 donne 55 avec V = 1

Calcul de L.

 

 

Essayons le 4 qui apparaît:

L715 x 37 = V7LL55

   715 x 37 = 26 455

 

L715 x 37 = V74455

La seule valeur de V qui convient est 1; alors L = 4

4 715 x 37 = 174 455

Avec 37 037

Idem précédemment.

Aucune possibilité pour obtenir le EE = 55

L7VE x 27 = V7LLEE

 

L7V5 x 27 = V7LL55

Solution unique

 

Résultat de l'exploration systématique des solutions possibles:

999 999 x LAVE = VALLEE x MAGMA

Avec l = v = m = 1

a une unique solution avec chiffres différents (Voir pannumérique).

 

 

 

  

DIVISION N°1

 

Question

 

P

H

I

L

I

L

I

L

H

I

L

T

I

L

S

H

I

L

H

I

L

0

0

0

 

Note

On pose la division complète, avec les calculs intermédiaires.

On donne le résultat de la multiplication

et on montre la soustraction effectuée

Ici:

H x IL = IL

PH - IL = T

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution

 

3

1

2

5

2

5

2

5

1

2

5

6

2

5

0

1

2

5

1

2

5

0

0

0

 

 

 

Explications

 

Première division:

H x IL = IL

H = 1

Fin 3e division:

L x L = ..L

L = 0, 1, 5 ou 6

3e division:

L x IL = 1 I L

L = 0 Pas possible (HIL, trois chiffres déférents)

L = 1 Pas possible (HIL n'est pas IL)

L = 6 Pas possible

Car: 6 x I6 = 1 I 6 pour I de 2 à 9 (valeur 1 déjà attribuée)

n'est pas possible

L = 5

Conclusions sur 3e division:

5 x I5 = 1 I 5

Si i = 2 => 1 I 5 = 125 Possible

Si i = 3 => 1 I 5 = 175 Possible

Si i = 4 => 1 I 5 = 225 Impossible

I = 2 ou 3

Situation

 

P

1

2,3

5

2,3

5

 

2,3

5

 

 

 

1

2,3

5

 

T

2,3

 

 

 

 

 

 

5

S

 

 

 

 

 

 

1

2,3

5

 

 

 

 

 

1

2,3

5

 

 

 

 

 

0

0

0

 

 

 

 

 

Valeur de S:

Si I = 3

S = unité de 3 x 5 = 5

Or 3 - S = 3 Pas possible

Si I = 2

S = unité de 2 x 5 = 0

Or 3 - S = 3 Possible

I = 2

S = 0

Suite:

Se déduit facilement, puisque l'opération complète est posée

 

 

P

1

2

5

2

5

 

2

5

 

 

 

1

2

5

 

T

2

 

 

 

 

 

 

5

0

 

 

 

 

 

 

1

2

5

 

 

 

 

 

1

2

5

 

 

 

 

 

0

0

0

 

 

 

 

 

 

 

 

DIVISION N°2

 

Question

 

N

E

L

L

Y

/

A

Y

 

N

L

Y

 

 

 

Y

F

Y

 

P

P

L

 

 

 

 

 

 

P

N

H

 

 

 

 

 

 

 

N

L

Y

 

 

 

 

 

 

N

L

Y

 

 

 

 

 

 

0

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution

 

 1

9

7

7

5

/

3

5

 

1

7

5

 

 

 

5

6

5

 

2

2

7

 

 

 

 

 

 

2

1

0

 

 

 

 

 

 

 

1

7

5

 

 

 

 

 

 

1

7

5

 

 

 

 

 

 

0

0

0

 

 

 

 

 

 

 

 

 

Suite

*    One two five eight

Voir

*    100 en chiffres et autres …

*    Nombres abcabc et ababab

*    Addition

*    Alphabet parlant

*    Anagramme de chiffres

*    Carré magique à deviner

*    Équation – Glossaire

*    Jeux – Index

*    Jeux avec nombres retournés

*    Sudoku

DicoNombre

*    Nombre 10 538

*    Nombre 999 999

*    Nombre  381 654 729

Site

*    Popular Web Sites for "cryptarithm"

Livre

*      Pour le plaisir de se casser la tête de  Louis Thépault
      Il comporte de nombreux cas avec leur résolution

      Passionnant!

Cette page

http://villemin.gerard.free.fr/Puzzle/lettdiv.htm