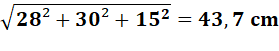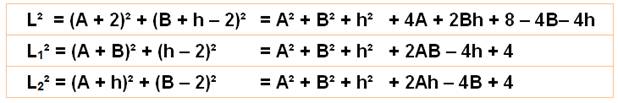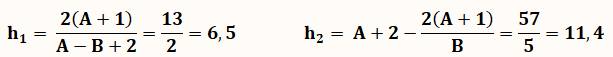Pavé: le chemin le plus court pour la fourmi

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/07/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	OBJETS 3D
Débutants Géométrie	VOLUMES				Glossaire Géométrie
INDEX Cylindre Géométrie Énigmes	Cube	Sphère	Cylindre		Cône
		Cylindre – Exercices		Fourmi sur cylindre creux
		Fourmi sur pavé		Fourmi sur cylindre plein
	Terminale	Sommaire de cette page >>> Fourmi sur pavé – D'un coin au coin opposé >>> Fourmi sur pavé – D'une face à une autre opposée >>> Bilan

PAVÉ – Trajet de la Fourmi

Parallélépipède

Comment déterminer les distances sur un pavé (ou parallélépipède)?

Cas où la fourmi et sa proie sont sur les coins opposés du pavé, et

Cas où le point de départ et d'arrivée sont quelconques sur les faces.

Voir Fourmi sur cube (exercice de seconde)

Devinette

Cent fourmis sont déposées au hasard sur un cylindre de 1 mètre de long. Elles avancent dans les deux directions à une vitesse de 1 mètre par minute. Arrivée en bout de course, elles tombent. Face à une autre fourmi, elles rebroussent chemin. Combien de temps attendrez-vous pour être sûr que toutes les fourmis sont tombées?

Solution

Fourmi sur pavé – D'un coin au coin opposé
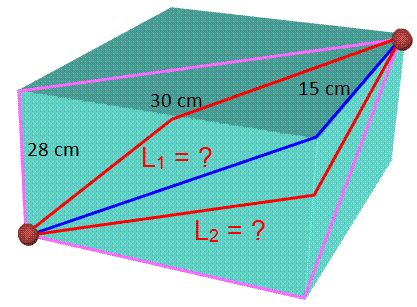
Sur ce pavé, une fourmi part d'un des points pour atteindre l'autre. Les chemins rouges sont naturellement plus courts que les autres. Mais lequel parmi les rouges est le plus court?
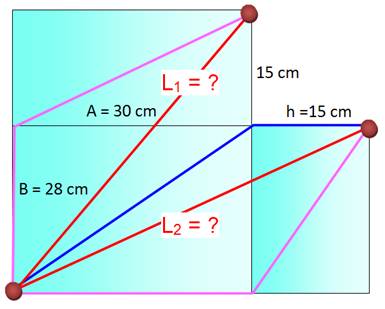
En développant (patron) les faces concernées, la géométrie est claire. La ligne droite s'impose. Avec le théorème de Pythagore, on en calcule la longueur.
Les longueurs, dans l'ordre: L = L1 = L = L2 = L = La fourmi doit être dotée d'un formidable flair pour choisir entre les deux trajets rouges. En effet, en passant par le haut plutôt que par le bas, elle ne gagnera que 0,6 cm. Attention, la diagonale du pavé droit (le chemin à vol d'oiseau, ou à vol de mouche, d'un sommet à son opposé) serait encore plus courte. L =
Conditions pour que L2 > L1 L1² = (B + h)² + A² = A² + B² + h² + 2Bh L2² = (A + h)² + B² = A² + B² + h² + 2Ah L2² > L1² si 2Ah > 2Bh ou encore A > B (ce qui est le cas de l'exemple).

Voir Brève 905

Fourmi sur pavé – D'une face à une autre opposée

Sur ce pavé, une fourmi doit rejoindre les deux points:

l'un est sur la face droite à une unité des arêtes du sommet arrière-droit-haut; et

l'autre est sur la face gauche à une unité des arêtes du sommet avant-gauche-bas.

Quel est le trajet le plus court?

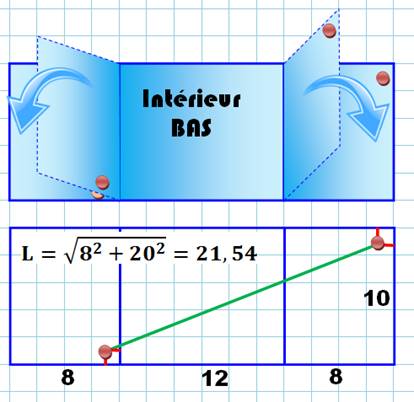
Une première idée consiste à développer la face du bas et ses deux faces latérales gauche et droite.

Notez bien que les deux points sont situés à l'extérieur de la boite; donc, en dessous sur ce dessin. Ce qui ne gêne pas pour calculer la longueur.

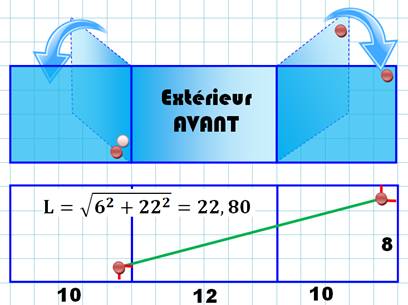
Ou alors, passons par l'avant. Pas plus court!

Notez bien que les deux points sont situés à l'extérieur de la boite; donc, au-dessus sur ce dessin.

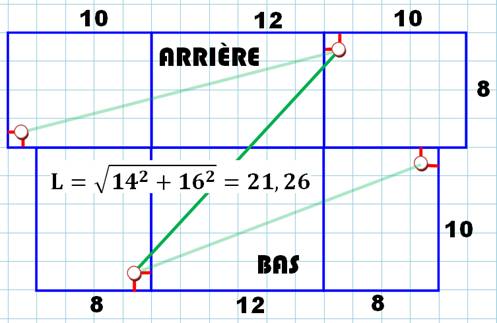
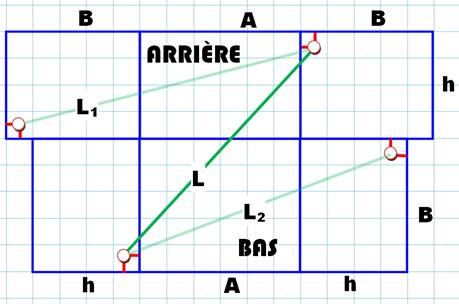
Peut-on faire mieux?

Oui, en faisant un développement mixte:

La face arrière est développée avec ses deux flancs.

La face du bas est développées avec les mêmes deux flancs.

Deux précautions pour relier les deux points:

ils doivent être du même côté, et

ils doivent relier deux flancs opposés.

Avec la disposition montrée, le trajet en vert foncé est le plus court. Il traverse quatre faces.

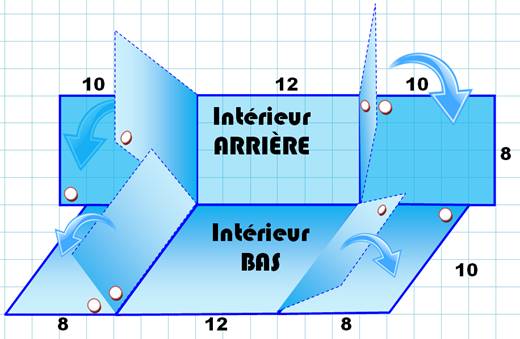
Nous montrons le point de vue intérieur, plus facile à imaginer par simple dépliement des faces. Les points sont en dessous, ce qui ne gêne pas le calcul des longueurs. Les flancs gauche et droit se retrouvent en double.

Cette disposition, traversant quatre faces, montre le trajet le plus court entre les deux points: 21,26 cm contre 21,54 et 22,80 pour des trajets impliquant trois faces.

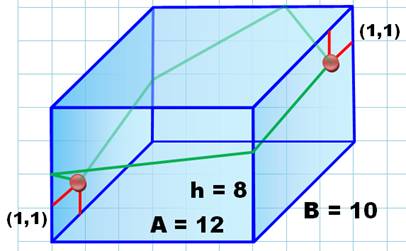
Est-ce toujours vrai? Comparons les distances:

Il est possible de comparer les parties différentes à droite. Pas facile!

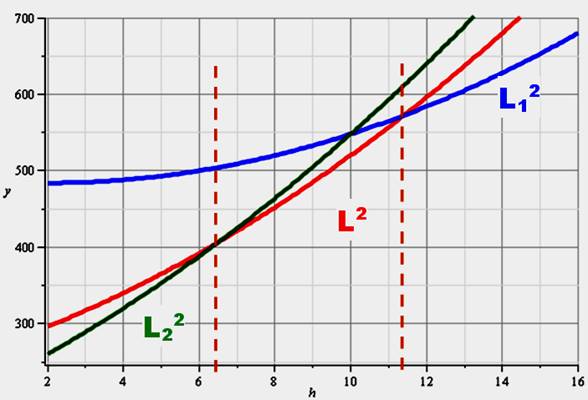
Voyons l'évolution sur un graphe.

Graphe y = L² = f(h) avec A = 12 et B = 10 cm

Valeurs de h₁ et h₂ (deux traits rouges pointillés) – Intersection des courbes

Commentaires

Nous constatons que notre exemple n'est pas si fréquent.

L n'est plus court que si h est compris entre 6,5 et 11,4 cm.

Merci à L.Z pour ses remarques

Bilan

Le trajet le plus court sur un parallélépipède se trouve facilement dans le cas où il faut rejoindre deux sommets. Par contre, lorsqu'il s'agit de rejoindre deux points quelconques sur les faces, il est conseillé d'être prudent.

Devinette – Solution

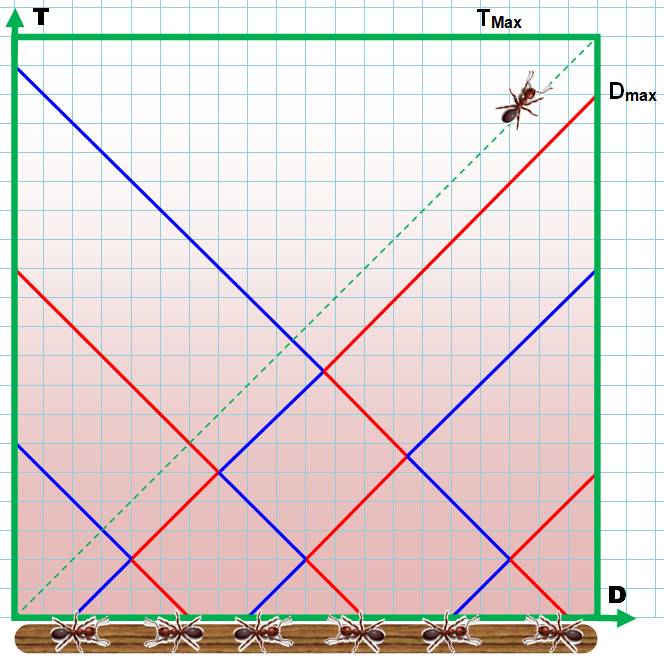
Les cent fourmis.

Une fourmi seule, déposée sur un bout de la baguette, mettra une minute pour atteindre l'autre bout et tomber (trait pointillé vert sur l'illustration).

Deux fourmis, chacune à une extrémité (cas critique) se rencontrent à mi-parcours et repartent en sens inverses et tombent. Durée une minute.

Trois fourmis, deux à un bout et la troisième à l'autre bout (cas critique), deux se rencontrent. Soit, un cas semblable à celui des deux fourmis. Durée maximale: une minute. Etc.

Avec cent fourmis: durée maximale: une minute.

Visualisation avec six fourmis:

Diagramme classique montrant la distance parcourue (D) par chaque fourmi en fonction du temps (T). La diagonale (trait pointillé vert) montre la trajectoire d'une fourmi seule déposée au bout gauche du bâton. Elle met T_max pour parcourir une distance D_max. Les six fourmis, du fait des rebonds, tombent bien avant T_max.

Notez que la pente des droites est une constante; elle représente la vitesse identique de chaque fourmi.