|
|||||||||||||||||||||||||||||||||||||||||
![]()
Le plus
|
Moïse
fit le dénombrement sur l'ordre de l'Éternel, en se conformant à l'ordre qui
lui fut donné. Le Livre des nombres – Bible |
Voir Pensées & humour
|
COMPTEZ
- DÉNOMBRER Trouver la quantité d'objets: les
compter un à un ou trouvez une méthode pour les recenser globalement ?
|
|
|
|||
|
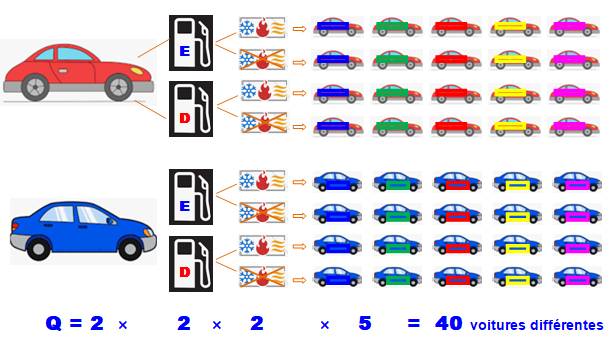
Achat de ma nouvelle voiture Le
concessionnaire me laisse le choix entre ces différents modèles équipés. Combien
de possibilités de choix ? |
Choix
|
||
|
Quels sont mes choix successifs ? |
|||
|
1. Je commence à choisir ma catégorie: 2 ou 4 portes |
|
||
|
2. Puis ma motorisation: essence ou diesel |
|
||
|
3. Mon choix de climatisation |
|
||
|
4. Mon coloris préféré |
|
||
|
Illustration
Exemple: la première ligne représente des cinq choix de
voitures à deux portes, à essence et AVEC air-conditionné.
La deuxième ligne, les cinq modèles à deux portes, à essence et SANS air-conditionné. |
|||
![]()
Explications
pas à pas
|
|
||||||||||||||||||||||||||||
|
Conclusion
|
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Conclusion
Ne soit pas jalouse Louise, on
aurait pu faire le même raisonnement avec toi ou avec Théo |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|||||||||
|
|||||||||
|
|
|
|
Papa souhaite en tirer une conclusion!
Au total,
|
|
|
|
|
|
Comparaison qui donne le vertige:
|
|
Voir Football / Quart de finale
|
|
||
|
Carré
Avec deux chiffres binaires, on peut écrire quatre nombres |
|
|
|
Cube
Avec trois chiffres binaires, on peut écrire huit nombres |
|
|
|
Compteur
|
Notez qu'en enroulant les réglettes sur elle-même, nous réalisons un compteur classique. Avec trois chiffres décimaux,
on peut écrire mille nombres. |
|
![]()
|
Suite |
|
|
Retour |
|
|
Je débute |
|
|
Voir |
|
|
|
![]()