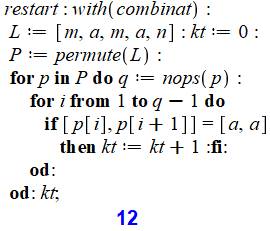|
|||||||||||||||||||||||||||||||||
![]()
|
ARRANGEMENENTS avec contraintes particulières On examine plusieurs cas avec contraintes
et on donne le dénombrement des possibilités. |
|
|
||
|
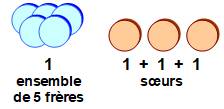
Ensemble 5 frères et 3 sœurs. |
Choix Tous assis
sur un banc. |
|
|
Contrainte |
Résultats |
|
|
Les frères sont
ensemble
|
Les frères forment un ensemble en soi Parmi
eux, il y a 5! permutations. Cet ensemble
de frères et les 3 sœurs forment 4
éléments que nous pouvons permuter. Soit 4! permutations. Le total des possibilités est 5! x 4! = 2 880 |
|
|
Les sœurs sont
ensemble
|
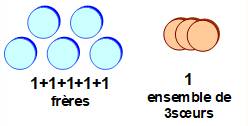
Les sœurs forment un ensemble en soi. Parmi
eux il y a 3! permutations. Cet ensemble
de sœurs et les 5 frères forment 6
éléments que nous pouvons permuter. Soit 6! permutations. Par principe multiplicatif: Le total des possibilités est 3! x 6! = 4 320 |
|
|
Aucune sœur à côté
d'une autre
|
Plaçons les 5 garçons: Il
y a 5! permutations. Les filles sont d'un côté ou de
l'autre des garçons. Il y a 6 possibilités (imaginer un
trou vacant entre les garçons et à chaque bout du banc: 4 trous et 2 bouts =
6 places possibles pour les filles). Il faut loger 3 filles parmi 6 places possible; soit
A36 arrangements:
6! / (6-3)! = 120. Par principe multiplicatif: Le total des possibilités est: |
|
|
Les sœurs sont aux
places paires |
Sur les 8 places (5 + 3), les filles
peuvent occuper les places 2, 4, 6 ou 8. Elles sont 3 pour ces 4 places; soit
A34 arrangements: 4! / (4-3)! = 24. Les
garçons occupent les places vacantes. Il y en a 5 pour les 5 frères: soit
5! permutations. Par principe multiplicatif: Le total des possibilités est: |
|
|
|
||
|
Ensemble 7 livres : 5 Dumas, 1 Hugo et 1
Voltaire. |
Choix Tous sur une étagère de ma
bibliothèque. |
|
|
Contrainte |
Résultats |
|
|
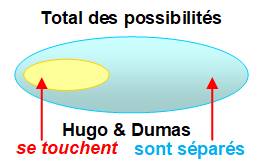
Hugo et Dumas sont
séparés
|
Ce
cas ne nécessite pas de calculs compliqués. Parmi les sept lettres [D, D, D, D, D,
H, V], il s'agit de placer H à un endroit sans contact avec D, ni à droite,
ni à gauche. Alors V ne peut pas être interne à
la suite des D, car alors H serait forcément voisin de D. Seules possibilités: H aux
extrémités. [H, V, D, D, D, D, D] [D,
D, D, D, D, V, H] Oui, mais avec d'autres lettres ou
plus ou moins de répétitions ? Oui, ça se complique ! Voir Analyse complète |
|
Merci à Antoine Sarrazin
pour avoir mis le doigt sur une grossière imperfection !
|
|
||||
|
Ensemble Lettres du mot MAMAN: 5 lettres dont: 2M, 2A, 1N. |
Choix Former tous les mots (sans nécessairement un sens). |
|||
|
Contrainte |
Résultats |
|||
|
Les voyelles ne sont
jamais ensemble |
Arrangements:
5! / (2! x 2!) = 30 Le
bloc AA peut prendre 4 positions parmi les 5 lettres. Les
trois autres lettres dont une doublée: 3! / 2! = 3 possibilités. Bilan
pour AA groupé: 4 x 3 = 12 |
|||
|
Programme de vérification Dans
P, on trouve les 30 arrangements des lettres de MAMAN. Pour
chacune (boucle en p), on cherche (boucle en i) le couple [a, a] et on
incrémente le compteur kt à chaque bonne pioche. La
valeur du compteur est imprimée en fin de traitement. Voir Programmation – Index |
|
|||
|
Ensemble Lettres du mot MATHEMATIQUES: 13 lettres dont: 2M, 2A, 2T, 2E soit 8 consonnes dont deux doubles
et 5 voyelles dont deux doubles. |
Choix Former tous les mots (sans nécessairement un sens). |
|
|
Contrainte |
Résultats |
|
|
Les voyelles ne sont
jamais ensemble |
Total
des arrangements en tenant compte des quatre éléments
multiples 13!
/ (2! x 2! x 2! x 2!) = 389 188 800 Cas
où les voyelles A A E E I sont ensemble. Il
y a en 5 dont 2 doubles: 5! / (2! x 2!) = 30 Ce bloc de 5 et les 8 consonnes dont 2 doubles forment: Cas
où les voyelles ne sont pas ensemble: 389
188 800 – 30 x 90 720 = 386 467 200 |
|
Voir Mathématiques
et ses domaines
|
|
|||
|
Ensemble Lettres du mot CONSTITUTION 12 lettres dont: 2O, 2N, 3T, 2I soit 7 consonnes dont 1 triple et 1
double et 5 voyelles dont 2 doubles. |
Choix Tous les mots (sans nécessairement un sens). |
||
|
Contrainte |
Résultats |
||
|
Les voyelles sont ensemble |
Cas
où les voyelles O O I I U sont ensemble: Il
y a en 5 dont 2 doubles: 5! / (2! x 2!) = 30 Ce bloc de 5 et les 7 autres lettres dont 1 triple et 1
double forment: Par
principe multiplicatif: Le
total des possibilités est : 30 x 3 360 = 100 800 |
||
|
Consonne puis voyelle … autant que possible Soit CVCVCVCVCVCC |
Approche avec MAMAN => MAMAN, MANAM et
NAMAN Permutations
de 3 consommes dont une double: 3!/2! = 3 Permutations
de 2 voyelles dont une double: 2!/2! = 1 Bilan:
3 x 1 = 3 cas de consonnes et voyelles alternées. Avec CONSTITUTION Permutations
de 7 consonnes dont 1 triple et 1 double: 7!
/ (3! 2!) = 420 Permutations de 5 voyelles dont 2 doubles: 5!
/ (2! 2!) = 30 Par
principe multiplicatif: Le
total des possibilités est : 420 x 30
= 12 600 |
||
|
Mots commençant et
finissant pas N |
On
place le N en début et fin du mot. Il
reste 10 lettres dont 1 triple et 2 doubles. 10! / (3! 2! 2!) =
151 200 |
||
|
|
|||
|
Ensemble 1, 2, 3, 4, 3, 2, 1 Soit 7 chiffres dont 3 doubles. Soit 4 impairs et 3 pairs |
Choix Tous les nombres. Il y a 7! / (2!x2!x2!) = 630
permutations |
||
|
Contrainte |
Résultats |
||
|
Les chiffres impairs
sont en positions impaires I,
P, I, P, I, P, I |
Il
y a 4 places pour positionner les nombres impairs. Il
y a 4 nombres impairs dont 2 doubles: 4!
/ (2! x 2!) = 6 Il
y a 3 places pour les 3 pairs dont 1 est double: 3!
/ 2! = 3 Par
principe multiplicatif: 6 x 3 = 18 |
||
|
Ensemble 1, 2, 4, 7, 8, 9 |
Choix Tous les nombres |
|||||
|
Contrainte |
Résultats |
|||||
|
Supérieurs à 70 000 sans chiffre répété
a = 7, 8 ou 9 |
Plaçons
le premier chiffre: A13
= 3! / 2! = 3 (OK évident sans passer par Apn !) Il
reste 5 chiffres à placer en 4 positions: A45
= 5! / (5 – 4)! = 120 Par
principe multiplicatif: 3 x 60 = 360 |
|
Ensemble 1, 2, 3, 4, 5 |
Choix Tous les nombres |
||||
|
Contrainte |
Résultats |
||||
|
Supérieurs à 2 000 sans chiffre répété
a = 2, 3, 4, 5 |
Plaçons
le premier chiffre: A14
= 4! / 3! = 4 Il
reste 4 chiffres à placer en 3positions: A34=
4! / 1! = 24 Par
principe multiplicatif: 4 x 24 = 96 |
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()