NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/05/2013 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	COMPTER
Débutants Compter FAQ	P-LISTE			Glossaire Compter
INDEX Combinatoire		P – Liste
		Sommaire de cette page >>> Approche >>> Nom >>> Illustration >>> Définition	>>> En pratique >>> Calculs >>> Applications >>> Nombres

P – LISTE

But

Choix d'individus parmi d'autres, y compris leurs clones.

Principe

Pour chaque choix, on peut prendre dans l'ensemble complet. On peut répéter les objets.

APPROCHE

Ensemble	Choix	Nom
{a, b, c, d}	aacd, bcad, …	p-liste de 4 parmi 4
	aac, bca, cda, ccb …	p-liste de 3 parmi 4
	aa, ab, bb, cd, db	p-liste de 2 parmi 4

L'ordre a son importance.

Un élément choisi, peut être réutilisé: c'est un tirage avec remise.

NOM
Une telle disposition s'appelle une p-liste de p objets parmi n un p-uplet un couple si p = 2 un triplet si p = 3 un mot de longueur p, une suite de longueur p.	Notation L^pn

ILLUSTRATION

Arrangement classique

Il s'agit de donner un rang
de 1 à p
à p parmi n objets.

	1^er	2^e
A
B
C
D

Ici est représenté l'arrangement BD.

Ce que permet la p-liste en plus

On peut donner le même rang au même élément.

	1^er	2^e
A
B
C
D

Ici est représenté l'arrangement BB.

DÉFINITION

Une p-liste d'éléments d'un ensemble E est une liste ordonnée de p éléments de E non nécessairement distincts. C'est un élément du produit cartésien E^p = E x E … x E (p termes).

Type de dispositions	Avec remise	Sans remise
Ordonné	p- liste	Arrangement & Permutation
Pas ordonné ou Simultané	p- suite	Combinaison

En pratique: Le COMPTEUR DÉCIMAL

L'image du compteur est bien pratique pour calculer la quantité de p-listes.

Prenons l'exemple des chiffres de 0 à 9 sur 3 positions. La valeur de chacune des positions est indépendante de la valeur de la position voisine:

La position de droite peut prendre toutes les valeurs de 0 à 9;

La position du milieu peut prendre toutes les valeurs de 0 à 9; et

La position de gauche peut prendre toutes les valeurs de 0 à 9.

En vertu du principe multiplicatif, le total des possibilités est le produit des possibilités individuelles. Ce qui en somme nous rassure, car ce que cela veut dire c'est que, avec 3 chiffres, on peut former 1000 nombres!

L³₁₀ = 10 x 10 x 10 = 10³

Les immatriculations

Avec les 26 lettres de l'alphabet, on forme une immatriculation de 3 lettres.

Combien d'immatriculations possibles ?

a

b

c

L³₂₆ = 26 x 26 x 26 = 26³ = 17 576

En binaire

En binaire les chiffres sont 0 ou 1.

Combien existe-t-il de nombres de 5 bits ?

0

1

1

L⁵₂ = 2x2x2x2x2 = 2⁵ = 32

Dénombrement
Le nombre de p-listes de n éléments est le nombre noté L^pn défini par:	L^pn = n^p

Exemples d'applications
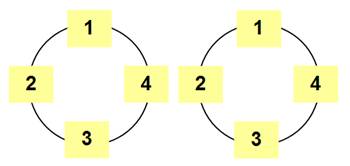
Les deux cercles On choisit un chiffre sur chaque cercle pour former un nombre de deux chiffres. On peut en former: L^24 = 4 x 4 = 16 nombres
La marelle On part d'un point de la couronne extérieure. On se dirige vers un des chiffres de la couronne intérieure. On peut parcourir: L^24 = 4 x 4 = 16 chemins

Nombres formés avec {1, 2, 3, 4}
Nombres formés avec {1, 2, 3} Nombres à un seul chiffre Nombres à deux chiffres Nombres à trois chiffres Nombres à quatre chiffres	L^13 = 3 possibilités L^23 = 3^2 = 9 L^33 = 3^3 = 27 L^43 = 3^4 = 81
Nombres formés avec {1, 2, 3, 4} Nombres à un seul chiffre Nombres à deux chiffres Nombres à trois chiffres Nombres à quatre chiffres	L^14 = 4 possibilités L^24 = 4^2 = 16 L^34 = 4^3 = 64 L^44 = 4^4 = 256
Nombres de trois chiffres avec le 4 au moins une fois = tous sauf les nombres à trois chiffres formés sans le 4.	L^34 – L^33 = 64 – 27 = 37
Nombres de trois chiffres avec une seule fois le 4 = le 4 positionné, il reste deux positions à remplier avec 3 chiffres, et ceci pour les trois positions du 4	3 x L^23 = 3 x 9 = 27
Nombres de trois chiffres avec plusieurs fois le 4 = le 44 positionné, il reste une position à remplier avec 3 chiffres, et ceci pour les trois positions du 44; sans oublier l'unique cas de trois 4. C'est aussi tous les cas sauf "pas de 4" ou "un 4"	3 x 3 + 1 = 10 64 – 27 – 27 = 10
Bilan pour les nombres à trois chiffres (positions) comportant les quatre chiffres (symboles).

Retour Suite	Combinatoire – Rubriques D'un coup d'œil
Voir	Cartes Compter les nombres Dés Dominos Échecs Factorielle et ses cousines Grenouilles Jeux Probabilités Triangle de Pascal
Cette page	http://villemin.gerard.free.fr/Denombre/Arralist.htm