|
||||||||||||||||||||||||||||||||||||||||
![]()
|
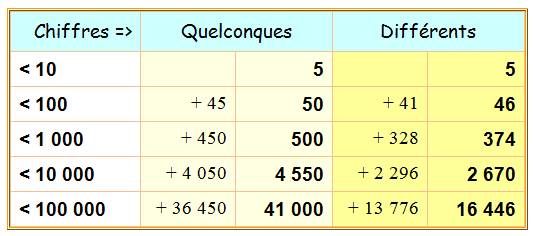
ARRANGEMENTS avec les NOMBRES Compter les chiffres pour
former les nombres divisibles par 2. |
|
|
||||||
|
Le calcul
direct est donné en bas de tableau. Le calcul
pas à pas permet de tracer la méthode pour le cas où les chiffres sont différents. Tous les chiffres
|
||||||
|
Contrainte |
Résultats |
Illustration En
rouge les interdits |
||||
|
1
chiffre |
Les chiffres pairs en excluant le 0
sont au nombre de 4. |
u = {0, 2, 4, 6, 8} => 4 |
||||
|
2
chiffres 10 12 … 18 20 22 … 28 … 90 92 … 98 |
Calcul pour chaque position des
chiffres:
Total: principe
multiplicatif: 5 x 9 = 45 |
u = {0, 2, 4, 6, 8}
=> 5 d = {0, 1,
2, … 9} => 9 |
||||
|
3
chiffres |
Calcul pour chaque position des
chiffres:
Total: principe multiplicatif: 5
x 10 x 9 = 450 |
u = {0, 2, 4, 6, 8}
=> 5 d = {0, 1, 2, … 9}
=> 10 c = {0, 1, 2, … 9} => 9 |
||||
|
TOTAL <
1000 |
Total de nombres inférieurs à 1000
divisibles par 2: 4
+ 45 + 450 = 499 |
Ce serait 500 si on
comptait le nombre
0 |
||||
|
Calcul
direct |
On considère les nombres à 3
chiffres, même s'ils commencent par des 0. On y trouvera également le cas 000,
libre à nous de l'exclure ou non. L'illustration montre les
possibilités, y compris le 000 Total: 5 x 10 x 10 = 500 |
u = {0, 2, 4, 6, 8}
=> 5 d = {0, 1, 2, … 9} => 10 c = {0, 1, 2, … 9} => 10 |
||||
|
|
||||||||
|
Contrainte |
Résultats |
Illustration En
rouge les interdits |
||||||
|
2
chiffres différents 22 44 … exclu |
Si l'unité est 0 la
dizaine est l'un des 9 chiffres (le 0 n'est pas possible): 9 possibilités Si l'unité est 2, 4, 6 ou 8 (4 cas) la
dizaine est l'un des chiffres, sauf celui déjà pris pour les unités et le 0
qui ne peut commencer un nombre: 8 possibilités Sous -total: 4 x 8 = 32 Total: principe additif: total des
nombres à 2 chiffres différents divisibles par 2:
|
d = {0, 1,
2, … 9} => 9
u = {0, 2, 4, 6, 8} => 4 d = {0, 1, 2, … u … 9 }
=> 8 |
||||||
|
3
chiffres tous
différents 100 110 112 … 122 144 … exclus |
Si l'unité est 0 les
deux autres sont choisis parmi les 9 autres chiffres que 0 soit
les arrangements de 2 parmi 9: A29 = 9! / 7! = 9 x 8 =
72 Si l'unité est 2, 4, 6 ou 8 (4 cas) la
centaine n'est ni 0 (jamais en début de nombre), ni le chiffre des unités restent 8
possibilités. la
dizaine n'est ni le chiffre des unités, ni le chiffre sélectionné pour les
centaines restent 8
possibilités. Sous-total: 4 x 8 x 8 = 256
possibilités de nombres à 3 chiffres différents terminés par 5. Total: principe
additif Total des nombres à 3 chiffres
différents divisibles par 2: |
d = {0, 1, 2, … 9} => 9 c = {0, 1, 2, … d … 9}
=> 8
u = {0, 2, 4, 6, 8} => 4 c = {0, 1, 2, … u … 9}
=> 8 d = {0, 1, 2, …5 … c … 9} => 8 Notez que
l'on examine les centaines avant les dizaines du fait du rôle non symétrique du 0 |
||||||
|
TOTAL <
1000 avec
des chiffres différents |
Total de nombres inférieurs à 1000 à
chiffres différents divisibles par 2 4 + 41 + 328 = 373 |
ou 374
avec le nombre 0 |
||||||
|
Vous pouvez
continuer le calcul en remarquant
|
|||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()