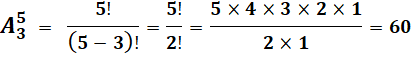arrangement, exemples

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/11/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants Compter	ARRANGEMENTS			Glossaire Combinatoire
INDEX Combinatoire		Général	Exemples	La moto
		Sommaire de cette page >>> Approche >>> Programme >>> Arrangements >>> Bilan >>> Table

ARRANGEMENTS - Exemples

Comment produire toutes les permutations avec un logiciel et en déduire les permutations de p parmi n.

Comment constituer une liste d'arrangements de p parmi n?

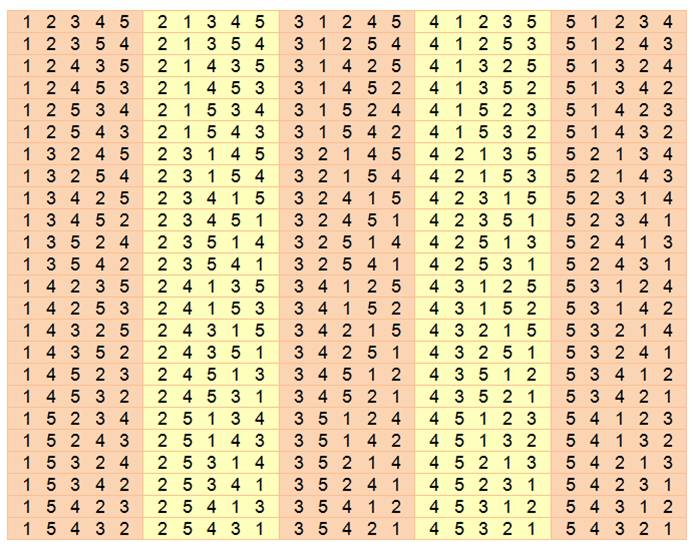
Si vous disposer d'un logiciel comme Maple, la solution est immédiate.

Ces deux instructions with(combinat); permute(5, 3) listent les arrangements de 3 parmi 5 (par exemple):

[[1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 2], [1, 3, 4], [1, 3, 5], [1, 4, 2], [1, 4, 3], [1, 4, 5], [1, 5, 2], [1, 5, 3], [1, 5, 4], [2, 1, 3], [2, 1, 4], [2, 1, 5], [2, 3, 1], [2, 3, 4], [2, 3, 5], [2, 4, 1], [2, 4, 3], [2, 4, 5], [2, 5, 1], [2, 5, 3], [2, 5, 4], [3, 1, 2], [3, 1, 4], [3, 1, 5], [3, 2, 1], [3, 2, 4], [3, 2, 5], [3, 4, 1], [3, 4, 2], [3, 4, 5], [3, 5, 1], [3, 5, 2], [3, 5, 4], [4, 1, 2], [4, 1, 3], [4, 1, 5], [4, 2, 1], [4, 2, 3], [4, 2, 5], [4, 3, 1], [4, 3, 2], [4, 3, 5], [4, 5, 1], [4, 5, 2], [4, 5, 3], [5, 1, 2], [5, 1, 3], [5, 1, 4], [5, 2, 1], [5, 2, 3], [5, 2, 4], [5, 3, 1], [5, 3, 2], [5, 3, 4], [5, 4, 1], [5, 4, 2], [5, 4, 3]]

Comme exercice vous pouvez programmer cette fonction (objet de cette page) >>>

Sinon, vous pouvez utiliser le tableur. Un exemple avec les arrangements de 4 parmi 9 (il y en a 3 024) est disponible en List4P9. Vous trouverez sur cette page Excel la façon de constituer une liste personnalisée. Je vous conseille de mettre votre tableur en route avant le téléchargement.

On ne mettra jamais suffisamment en garde les utilisateurs qui voudraient utiliser ces listes pour tester toutes les combinassions de cadenas ou autre. En supposant 10 secondes par test, il faudra 9 heures pour balayer tous les cas possibles de 4 chiffres pari 9.

Approche

Nous souhaitons lister toutes les permutations des nombres 1, 2, 3, 4, 5 représentant cinq objets à permuter.

Nous avons que la quantité de permutations est égale à 5! = 120.

Remarquons, pour bien faire la différence, que nous souhaitons des permutations: les cinq nombres sont différents (2, 1, 4, 3, 5 par exemple).

Si nous avions autorisé les répétions de chiffres (comme 1, 1, 2, 2, 5) nous aurions: 5⁵ = 3 125 lignes dans la p-liste.

Comment reconnaître les cas de répétition des nombres.

Un critère nécessaire est que la somme des termes de la liste soit égale à: 1 + 2 + 3 + 4 + 5 = 15.

Ce n'est pas suffisant du fait que 1 + 2 + 2 + 5 + 5 = 15 ou 1 + 1 + 3 + 5 + 5 = 15. Il faut éliminer ces cas. Un moyen consiste à exiger que la liste comporte au mois un 1 et un 2 et un trois.

Programme

Voici le programme commenté et le résultat de son éxecution:

Arrangements

La quantité de permutations est bien 120 comme le montre la valeur du compteur.

La liste permet d'identifier, que les arrangements de trois parmi 5, par exemple, sont systématiquement présents deux fois dans la liste: comme 12345 et 12354. Leur quantité est égale à 120 / 2 = 60.

Ce que nous confirmons par le calcul: