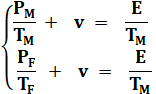NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	ÉNIGMES
Débutants Vitesse	Durée				Glossaire Vitesse
INDEX Jeux	Escalier	Tonneau	Robinets	Nénuphar
	Escalier (double)	Travaux	Vitesse	Horloge
		Sommaire de cette page >>> Deux copains >>> Gain avec escalier roulant >>> Un aller-retour >>> Moi et mon fils >>> Escalier mécanique >>> je monte >>> Mon fils monte aussi >>> Problème n°1 >>> À contre-sens >>> Problème n°2 >>> Problème N°3 >>> Solution par raisonnement

ESCALIER ROULANT

Escalier mécanique / Escalator

Plusieurs personnes gravissent l'escalier mécanique en des temps différents. À partir de ces données, il faut trouver la taille de l'escalier. Ou alors comment se comportera une personne qui prend l'escalier à contre-sens?

Comment résoudre à coup sûr ce genre de problème? Voici les solutions pour quelques unes de ces énigmes, illustrées pas à pas.

Escalier mécanique.

Escalier roulant.

Escalier mobile.

Anglais: Escalator (qui est une marque)

Escalier dont les marches sont mobiles permettant aux personnes de franchir les niveaux d'un immeuble sans effort.

Deux copains et escalier fixe
Deux copains montent une volée d'escaliers. L'un s'estime plus sportif et laisse son copain partir une demi-minute avant lui. Il grimpe 50 marches par minute, alors que son copain a un rythme de 25.	Formule générale: M = V.T Pour le moins rapide: M = 25/60 T Pour le plus rapide qui attend: M = 50/60 (T – 30) Pour la même quantité de marches: 25/60 T = 50/60 (T – 30) Résolution: T = 60 secondes et M = 25 marches

Gain avec escalier roulant
Je monte l'escalier à l'arrêt en 3 minutes. Immobile sur l'escalier en fonctionnement je monte en 1 minute. Combien de temps si je marche sur l'escalier en mouvement ?	Vitesse de l'escalier: M / 180 Vitesse du passager: M / 60 Vitesse du passager sur l'escalier = somme des vitesses: M/180 + M/60 = M/45 Mon temps de montée, aidé de l'escalator, est réduit à 45 secondes.

Un aller-retour
Je monte sur un escalator en marche et compte 50 marches pour arriver en haut en marchant à raison d'une marche par seconde. Je descends cet escalator en 125 marches à la vitesse de 5 marches par seconde	On note M la quantité de marches et v la vitesse de l'escalator. À la montée, je mets 50 secondes: L – 50 v = 50 À la descente, je mets 25 secondes: L + 25 v = 125 En résolvant ce système d'équations: par soustraction: 25v + 50v = 125 – 50 = 75 => v = 1 v = 1 marche /seconde et L = 100 marches.

Moi et mon fils – Combien de marches ?

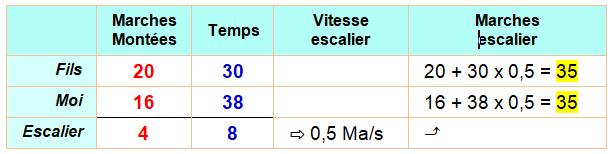
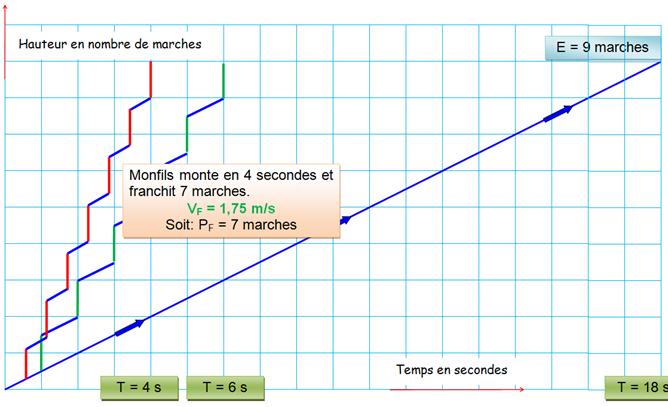
Énigme (simple) Mon fils monte 20 marches et met 30 secondes pour arriver en haut de l'escalier roulant en marche. Moi, je monte 16 marches et mets 38 secondes. Combien l’escalator comporte t-il de marches ? Solution Mon fils gagne 8 secondes (38 – 30) pour 4 marches (20 – 16). L'escalier progresse à la vitesse de 1 marche en 2 secondes, soit une vitesse propre de l'escalier: v = 0,5 marche/s. En 30 secondes, je monte 20 marches et l'escalier progresse de 30 x 0,5 marches, soit 20 + 15 = 35 marches pour l'escalier au repos du bas en haut (sans compter les marches cachées). Je vérifie avec mon fils: 16 + 38 x 0,5 = 35 marches. 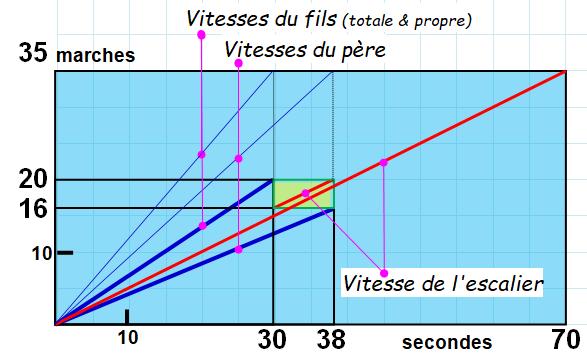En résumé Note: seul, l'escalier met 35 x 0,5 = 70 secondes pour faire la montée. Illustration Malgré tout, je voudrais me rassurer complètement. Est-ce que mon raisonnement est le bon ? Y-a-t-il un piège ? Rien ne vaut un graphique "temps en fonction de la distance", en se souvenant que la pente de la droite est égale à la vitesse. En petits traits bleus, la vitesse totale (avec celle de l'escalier) du fils et du père: 35 marches en 30 et 38 secondes. En gros traits bleus, la vitesse propre de chacun: 20 marches en 30 secondes et 16 en 30 secondes. La grande diagonale rouge montre la progression de l'escalier: 35 marches en 70 secondes (connue après avoir trouvé la solution). Le carré jaune montre les écarts (utilisés pour notre raisonnement) et, la diagonale donne bien la vitesse de l'escalator (parallèle à la grande diagonale rouge).

Note: "Ma femme et moi" peuvent être remplacés par deux prénoms

comme "Alice et Bob" (pour deux prénoms en A et B)

Méthode de résolution dans le cas général

Escalier mécanique

Prenons un escalier roulant. Au repos vous constatez qu'il comporte 9 marches visibles pour couvrir la hauteur du rez-de-chaussée au premier étage (E = 9 marches) Mis en route, vous vous placez sur la première marche. Sans bouger, vous chronométrez T = 18 secondes pour atteindre le premier étage. Conclusion l'escalier progresse d'une marche toutes les 2 secondes ou autrement dit: sa vitesse (v) est de 0,5 marche par seconde.

IMPORTANT

Nous voilà dotés des outils pour raisonner sur ce genre de problème.

un diagramme qui montre la distance parcourue (ici E) en fonction du temps (t).

une formule primordiale: longueur égale vitesse multipliée par le temps: L = v.t (ici: E = v. t => 9 = 0,5 x 18).

Voir Problèmes sur les vitesses

Je monte

L'escalier mécanique est en marche, et je monte les marches pour arriver plus vite en haut. Je mets exactement 6 secondes. Et je constate que j'ai eu à faire seulement six pas (Mes pas: PM = 6). L'escalier poursuit son ascension à la vitesse d'une demi-marche par seconde (trait oblique bleu); quant à moi, toutes les secondes, je monte d'une marche (trait vertical vert). Attention: je ne confonds pas les 6 pas (marches) que je monte et les 9 marches qui séparent le rez-de-chaussée du premier étage. 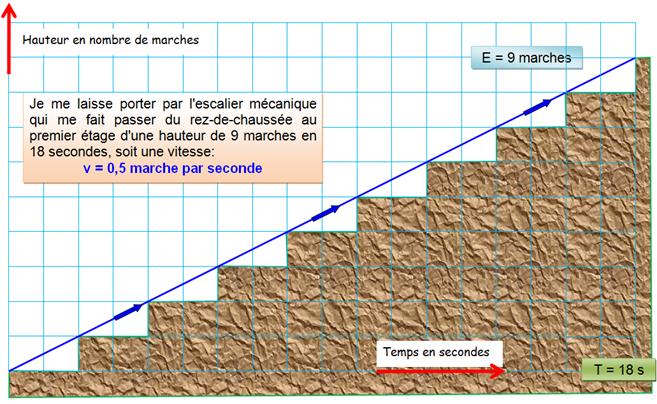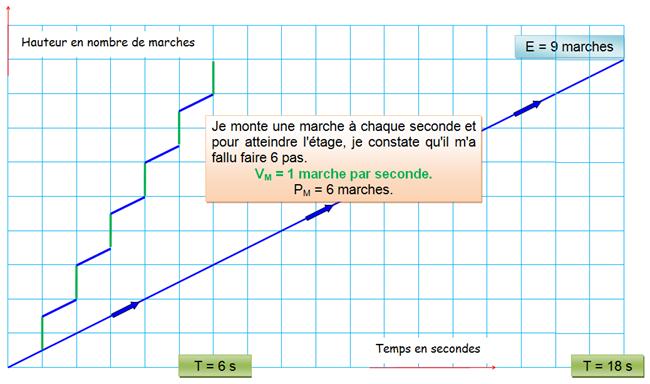Bilan des vitesses: vitesse de l'escalier: v = 0,5 ma/s ma vitesse propre: VM = 1 ma/s vitesse totale: V = 1,5 ma/s Formulation E = (VM + v) T 9 = ( 1 + 0,5) 6 pour notre exemple

Mon fils monte aussi
Mon fils est rapide. Il monte 7 marches et arrive en haut en 4 secondes Bilan des vitesses: vitesse de l'escalier: v = 0,5 ma/s vitesse propre de mon fils: VF = 7/4 = 1,75 ma/s vitesse totale: V = 2,25 m/s Formulation E = (VM + v) T 9 = ( 1,75 + 0,5) 4 pour notre exemple

Problème 1 (basé sur l'exemple ci-dessus)

Énoncé (données) Seules données: Moi, j'arrive en haut en 6 secondes et 6 marches Mon fils arrive en haut en 4 secondes et 7 marches Combien de marches pour couvrir la hauteur entre le rez-de-chaussée et le premier? Quelle est la vitesse de l'escalator? Solution Si on me dit que j'arrive en haut en montant PM = 6 marches en TM = 6 secondes, cela veut dire que ma vitesse propre VM = PM / TN = 6/6 = 1 marche par seconde. Pour mon fils sa vitesse propre est VF = PF / TF = 7/4 = 1,75 marche par seconde. Rappel: Je cherche à calculer E et v et je connais pour le moment: VM = PM / TN = 6/6 = 1 VF = PF / TF = 7/4 = 1,75 Appel à notre formule fondamentale E = vitesse par temps ou plus pratique ici: vitesse = E / temps. Traduction pour moi et mon fils: VM + v = E / TM => 1 + v = E / 6 VF + v = E / TF => 1,75 + v = E / 4 Pour éliminer v de ces deux équations; il suffit de retrancher l'une de l'autre 0,75 = E/4 – E/6 0,75 = E/12 E = 12 x 0,75 = 9 marches de hauteur. v = E/6 – 1 = 9/6 – 1 = 0,5 marche par seconde. Bilan Connaissant temps et nombre de marches pour deux personnes, il est possible d'en déduire les caractéristiques de l'escalier roulant. Deux équations semblables: l'une pour Moi (M) et l'autre pour mon fils (F). En retranchant l'une de l'autre, v est éliminé et la valeur de E se calcule immédiatement.

À contre-sens
Amaury est un peu espiègle et prend l'escalator à contre-sens. Il part du premier étage et chaque fois qu'il descend d'un pas, l'escalator remonte d'une demi-marche. Formulation: PA / TA – v = E / TA 18 / 18 – 0, 5 = 9 / 18 dans notre exemple

Problème 2 – Vu sur Internet

Données Dans un magasin, un escalier roulant permet de passer du rez-de-chaussée au 1^er étage. Mélanie monte 20 marches et atteint le haut en 15 secondes. François monte 22 marches et atteint le haut en 12 secondes. Amaury, à contre-sens, le descend en 18 secondes. Combien Amaury a-t-il descendu de marches ? Solution En deux temps: d'abord trouver les paramètres de l'escalier roulant: E (hauteur de l'étage en quantité de marches) et v (vitesse de l'escalier en marches par seconde). Premier temps (formules ci-dessus): PM / TM + v = E / TM => 20/15 + v = E / 15 PF / TF + v = E / TF => 22/12 + v = E / 12 Soustraction 22/12 – 20/15 = = E/12 – E/15 11/6 – 4/3 = (15E – 12E) /180 3/6 = 3E / 180 E = 0,5 x 180 / 3 E = 30 marches. v = 30/15 – 20/15 = 2/3 marche / seconde. Cas d'Amaury qui va à contre sens PA / TA – v = E / TA PA / 18 – 2/3 = 30 / 18 PA / 18 – 12/18 = 30 / 18 PA = 30 + 12 = 42 marches

Énigme présente sur Internet avec 3 chatons ou encore un gamin qui s'amuse sur l'escalator

Problème 3

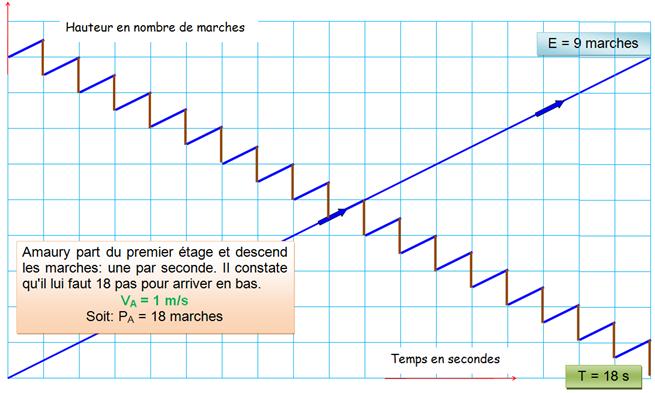
Données Sur un escalier roulant, un jour en marchant à la vitesse V, je compte 10 marches. Le lendemain en courant à la vitesse 2V, je compte 16 marches. Combien y-a-t'il de marches?  Solution Formulation: vitesses V = P1 / T1 => V = 10 / T1 2V = P2 / T2 => 2V = 16 / T2 16 / T2 = 20 / T1 T2 = 4/5 T1 Formulation: équations E = ( V + v) T1 = (10 / T1 + v) T1 = 10 + v / T1 E = (2V + v) T2 = (16 / T2 + v) T2 = 16 + v / T2 = 16 + 5/4 v / T1 v / T1 = E – 10 v / T1 = 5/4 (E – 16) E – 10 = 5/4 (E – 16) 5/4 E – E = 5/4 16 – 10 1/4 E = 10 E = 40

Voir Solution rapide pour une énigme semblable

Solution du Problème 3 – Alternative
Données Sur un escalier roulant, un jour en marchant à la vitesse V, je compte 10 marches. Le lendemain en courant à la vitesse 2V, je compte 16 marches. Combien y-a-t'il de marches?  Solution Pour résoudre le problème, une solution par raisonnement consiste à imaginer une paire de jumeaux, l'un à V et l'autre à 2V.
Jumeau 2V (Deuvé)	Jumeau V (Unvé)
Deuvé monte 2k marches par seconde (2V).	Unvé monte k marches par seconde (1V)
En haut, Deuvé a monté 16 marches.	À ce moment là, Unvé a monté 8 marches.
Pendant ce temps, Deuvé et Unvé ont été élevés du même nombre de marches par l'escalier roulant.
	Sans l'aide de l'escalier, Unvé aurait encore à monter 8 marches. Or, il ne lui en reste que 2.
Soit l'avance de l'escalier;	2 marches montées pour 8 parcourues avec l'escalier
Et, la solution:	10 marches montées 40 marches parcourues avec l'escalier.
Illustration Notez qu'avec les données fournies, l'échelle du temps n'est pas connue.

Suite	Escalier roulant avec lui à double vitesse de l'autre (suite et autres méthodes de résolution) Tonneau Voir en-tête
Voir	Contenance – Bouteilles Escalier Paquebot de Lucas Progression géométrique
Cette page	http://villemin.gerard.free.fr/aJeux1/Temps/escalier.htm