|
||||||||||||||||||||||||||||
![]()
|
|
|||
|
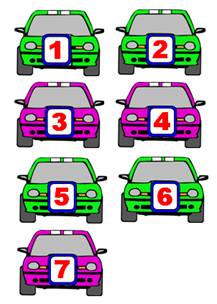
Énigme simple Dans ma
boite de jeu, j'ai sept voitures miniatures numérotées de 1 à 7. Je veux
en choisir cinq, mais il ne doit pas y en avoir deux avec des numéros ayant
une différence de 2. Puis-je relever
ce défi? Une initiation pour résoudre l'énigme suivante … |
Illustration
|
Solution Je choisis la voiture 1 et la voiture 2 (vertes). Je laisse les voitures 3 et 4 (roses) car distantes de 2 avec les deux
premières. Je choisis la voiture 5 et la voiture 6 (vertes). Soit quatre voitures
sélectionnées. Me reste la voiture n°7 (rose), mais elle est incompatible avec la
voiture 5 (verte). Je ne peux pas relever le défi! En prenant d'autres numéros, je retrouverai toujours cette
incompatibilité. Essayez! |
|
|
|
||
|
On
dispose de 120 tableaux numérotés de 1 à 120 On
souhaite en sélectionner 64 pour une exposition. Pour des
raisons de superstition, pas de tableaux avec des numéros avec une différence
de 7. Est-ce
possible? |
Si le tableau n° 20 est dans l'exposition, alors les tableaux n°13 et
n°27 n'y sont pas car la différence est égale
à 7. |
|
![]()
|
|
||
|
Solution quasi-muette (voir
l'illustration) Remarquons
qu'il est possible de sélectionner 63 tableaux en neuf groupes de 7. Et d'en
laisser 56 en réserve, lesquels peuvent être regroupés en 8 groupes de 7. Soit un
total de 119 tableaux, sachant qu'il en manque 1 pour avoir notre compte dans
la galerie. Numérotons
tous ces tableaux de 1 à 7 puis 15 à
21 etc. pour les groupes verts sélectionnés; et de 8 à 14, puis de 22 à 28,
etc. pour les groupes rouges de réserve. La consigne est respectée: pas de
tableaux sélectionnés dont les numéros sont espacés de 7 (exclusion des
groupes rouges).
Avec
cette démarche, il ne reste plus que des numéros interdits. Impossible de
sélectionner le 64e tableau pour l'exposition. Note: il n'y a pas de perte de généralité en numérotant les tableaux comme
nous venons de le faire. |
||
|
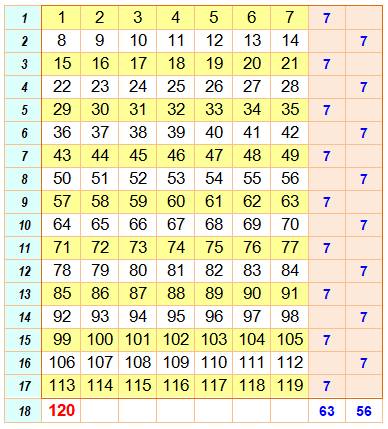
Autre solution avec tableau Répartis comme
sur cette table les numéros sur une ligne sont bien espacés de 7 avec ceux
des lignes voisines (pour la même colonne). En jaune
les groupes de tableaux sélectionnés et en blanc ceux mis en réserve. Tout est
sympathique jusqu'au tableau n°119 avec 63 tableaux sélectionnés. En
revanche, impossible de sélectionner un nouveau tableau (le 64e)
pour l'exposition. Celui qui reste est sur une ligne blanche interdite. |
|
|
Merci
à Alain Rodot pour cette énigme
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()