|
||||||||||||||||||||||||||||||||||||||||
![]()
|
LOTO traditionnel avec cartons Loto familial Présentation générale et Règles de
rédaction Jeu qui
se joue en société selon une règlementation stricte. Le jeu le plus classique
consiste à distribuer quatre cartons à chaque joueur. Le maitre du jeu tire
des boules numérotées de 1 à 90 et annonce son tirage. Sont gagnants les
premiers à remplir: une ligne (quine), deux lignes ou le carton plein. Quelle
est la quantité de cartons différents ? On procèdera en deux étapes:
|
Anglais: Bingo / Bingo Lotto Lottery with tickets / Tambola
ticket
Vocabulaire
|
Loto traditionnel ou loto
familial: celui qui se joue avec des cartons à remplir. Jeu de 6 ou 96 cartons: six cartons avec nombres de 1 à 90; ou 96 avec 16
fois ces nombres. Carton éligible ou
valide: qui respecte les règles du loto
traditionnel. Configuration: carton
du loto muet, sans les nombres. |
Ce que nous
allons calculer sur ces pages

Voir Nombres
en 10 puissance 21
|
Vers 1530, en Italie apparait une sorte de loterie: Lo Giuoco del Lotto d'Italia. Il arrive en France
vers 1770 sous le nom de Le
Lotto, joué par l'aristocratie, puis se propage en Europe et
Grande-Bretagne. L'Allemagne utilise une version de ce jeu pour l'enseignement. En 1920, Hugh J. Ward s'inspire des jeux de foire,
écrit un traité décrivant les règles du jeu, et dépose un copyright. En 1942, Erwin S. Lowe dépose le brevet des cartons du
loto moderne. Le jeu s'appelait Beano (joué avec les haricots: beans en
anglais) et, il a connu un succès fulgurant. Un jour, une dame enthousiaste
cria "bingo" au lieu de "beano", et le jeu devint le Bingo. L'Église se mit à utiliser ce jeu pour lever des fonds
(10 000 jeux de Bingo par semaine vers 1934 en Amérique). Cette façon de proposer un nombre et de le retrouver
sur un carton est appliquée depuis longtemps pour apprendre à calculer (tables de
multiplication ou encore fractions). |
![]()
|
|
||
|
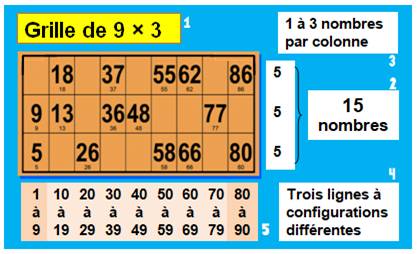
Loto traditionnel ou familial 1) Un carton du loto traditionnel est une grille de 9 x 3 = 27 cases. 2) Chaque ligne comporte cinq nombres, pour un total de quinze. 3) Chaque colonne montre un, deux ou trois numéros. 4) La présence de nombres est différente d'une ligne à l'autre. 5) Le nombre dans une case est choisi de 1 à 90, non répétés. |
La grille du loto et sa composition
Source image du carton: cartaloto.net |
|
|
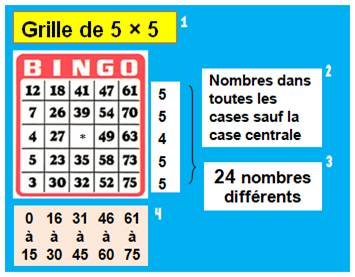
Loto Bingo Américain 1) Un carton du loto Bingo américain est une grille de 5 x 5 = 25 cases. 2) Chaque ligne comporte cinq nombres, pour un total de quinze, sauf
celle du milieu, 3) Soit 24 nombres parmi les nombres de 1 à 75. 4) Les colonnes sont nommées B, I, N, G et O et les nombres inscrits sont
choisis dans une plage de 15 nombres. |
La grille du loto BINGO et sa
composition
|
|
But de ces pages
|
Notre but est de calculer
la quantité de cartons pour chacun de ces jeux de loto. Autant, le loto
américain conduit à un calcul simple de
combinatoire, autant, le loto traditionnel européen entraine des calculs
assez complexes. Ce que nous nous proposons de développer sur ces pages. Pratiquement aucune
littérature Internet sur le sujet (à ma connaissance). |
|
|
||
|
Règles 1 et 2 Un carton du loto traditionnel est une grille de
9 x 3 = 27 cases. Chaque ligne comporte cinq nombres, pour un total
de quinze. On appelle CONFIGURATION,
la disposition des nombres sur le carton du loto sans en préciser la valeur. |
Une configuration montre l'emplacement des nombres
|
|
|
Règle 3 Il y a 1, 2 ou 3 nombres sur une colonne; jamais
zéro. La probabilité de trouver trois nombres dans une
colonne est assez faible. Les nombres dans une colonne sont
interchangeables. Par exemple, dans la colonne 1, les nombres 5 et
6 peuvent être inversés et les deux cartons sont considérés comme identiques. En Europe, les nombres semblent mis dans un ordre
quelconque, alors qu'en Amérique, ils sont placés par ordre décroissant du
haut vers le bas. Notez la mathématique de la quantité
de nombres par colonne. Alors, la somme vaut naturellement 9. Du fait qu'il n'existe pas de colonne vide, sur
deux colonnes, il faut placer 10 nombres sur 9 colonnes. Il y a
nécessairement au moins une colonne avec deux
nombres (principe
des tiroirs). En plaçant 15 nombres dans 9 colonnes, il y a six
cas de colonnes à deux nombres. Une colonne avec trois nombres compte double. |
|
|
|
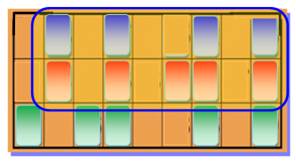
Règle 4 Les configurations des lignes sont différentes. Quelle que soit la valeur des nombres, on ne peut
pas, par exemple, avoir tous les
nombres sur les 5 premières colonnes. On se souvient que:
|
Exemple de configuration exclue
Exemple de configuration valide
(éligible)
|
|
|
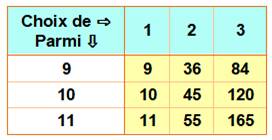
Règle 5 Elle induit une disparité des quantités de
nombres possibles dans chaque colonne: En colonne 1, on choisit des nombres parmi 9; En colonnes 2 à 8, des nombres parmi 10; et En colonne 9, des nombres parmi 11. Le calcul de la quantité de cartons devra prendre
en compte les neuf cas du tableau. |
Toutes les
possibilités de choix pour les colonnes
Exemple: combinaisons de 3 parmi 11
Voir
Combinaisons |
|
Exemples de cartons du loto traditionnel: éligible ou non

|
|
||
|
Première étape: Quantité de configurations |
On
appelle configuration, la disposition des
cases comportant des nombres, quelle que soit la valeur du nombre. Le but est
alors de trouver la quantité de configurations éligibles.
Note sans les
exclusions, on a trois fois les combinaisons de 5 parmi 9, |
|
|
Deuxième étape: Quantité totale de cartons |
On
attribue un nombre à chacune des cases et on calcule la quantité totale de
cartons qu'il est possible de composer.
Source image: Jeu de
société Loto Dujardin Note pour se
faire tout de suite une idée de la quantité phénoménale de cartons: En conservant toutes les
colonnes identiques sauf la première: la
case de la ligne 1 peut prendre les 9 valeurs de 1 à 9, la case de la ligne 2
également; tout comme celle de la ligne 3: on a déjà 9 x 9 x 9 = 729 cartons
différents. Ajoutez les cas où il y a
deux nombres ou trois nombres dans la colonne et on monte à plus de 300 000
possibilités pour le remplissage de la seule première colonne (les nombres
sont dans un ordre quelconque => 9 x (9x8) x (9*8*7) = 326 592). La page
3 vous indiquera le calcul précis. |
|
Merci à René Brocas pour l'idée
de cette page et pour contribution
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette
page |
![]()