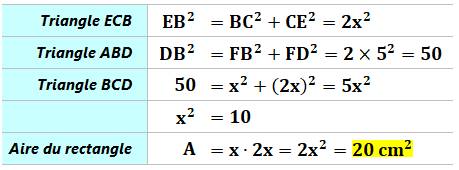Demi-cercle et rectangle

Édition du: 04/12/2024

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Fourmi sur un pavé	Défis divers

Demi-cercle et rectangle

Problèmes rencontrés sur le Net proposés comme défis aux Internautes.

Problème qui semble insoluble. Notez qu' l'on cherche l'aire et non pas toutes les longueurs.

Sommaire de cette page

>>> Le demi-cercle et le rectangle défi n°1

>>> Le demi-cercle et le rectangle défi n°2

>>> Triangle rectangle dans demi-cercle

Débutants

Géométrie

Glossaire

Géométrie

Le demi-cercle et le rectangle (défi n°1)

haut

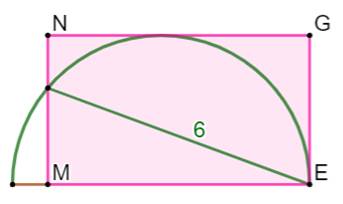
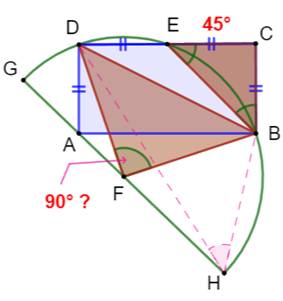
Problème

Trouver l'aire du rectangle MNGE.

Seule la dimension de la corde verte est connue (6).

Solution

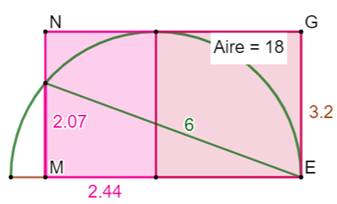
Voir Théorème de Pythagore
Équation du cercle

Commentaires

En bas, une figure possible avec les véritables proportions.

Si, pour cette figure, l'aire est connue, les longueurs x et y ne sont pas déterminées.

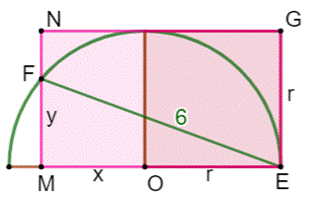
Données

Notations

Exemple avec mesures pour x et y

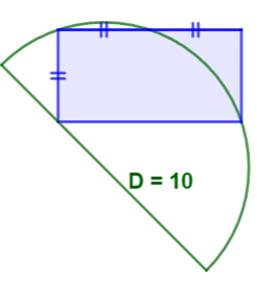
Le demi-cercle et le rectangle (défi n°1)		haut
Construction Un rectangle avec L = 2l. Un demi-cercle de 10 cm de diamètre avec: le diamètre passant par un sommet la circonférence passant par deux sommets et un point milieu du rectangle. Quelle est l'aire du rectangle ? Pistes Pensons à trouver des triangles rectangles pour y appliquer le théorème de Pythagore. Candidats: BCE, BCD et BDF, à condition de montrer que l'angle BFD est droit. BFD droit ? On peut en avoir une intuition en construisant la figure exacte avec GeoGebra. Lorsqu'il est question d'angles en présence d'un cercle, on pense aux propriétés des angles inscrits et des angles au centre. Solution Le triangle rectangle BCE a deux côtés égaux, il est aussi isocèle. Ses angles à la base valent 45°. L'angle BED vaut 180° – 45° = 135°. L'angle inscrit BHD intercepte le même arc mais dans l'autre sens; il vaut 180° – 135° = 45°. L'angle au centre BFD, interceptant le même arc, vaut le double: 90°. Posons x = BC = CE = DE = AD.	Données Notations
Calculs

Triangle rectangle dans demi-cercle		haut
Problème assez simple à condition de se souvenir du théorème d’Euclide dans le triangle rectangle : le carré d’un côté de l’angle droit est égal au produit de l’hypoténuse par la longueur du segment découpé par la hauteur sur l’hypoténuse.
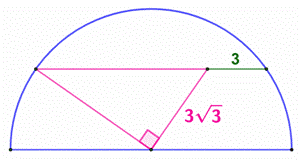
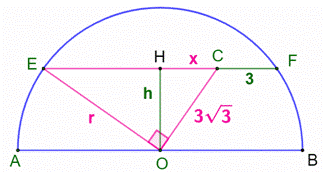
Construction Un demi-cercle et une corde parallèle au diamètre. Un rayon et sa perpendiculaire. La figure indique les mesures relevées. Quelle est l’aire du demi-cercle ? Longueur du segment EC (Voir la figure du bas) On trace la hauteur OH, alors: HE = HF et EC = x + 3 + x = 2x + 3 Puis, on applique le théorème d’Euclide : OC² = HC ٠ HE (3√3)² = x (2x + 3) 27 = 2x² + 3x dont la racine positive est x = 3 Alors EC = 2x + 3 = 9 Longueur de r Théorème de Pythagore dans le triangle OCE : (3√3)² + r² = 9² r² = 81 – 27 = 54 Aire du demi-cercle A = 1/2 π r² = 27 π	Figure initiale Figure avec notations

Retour	Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	How to Solve Tricky But Beautiful Application of Properties of Circles, Quadrilaterals, Triangles – Math Avenue – Vidéo
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CerRecta.htm