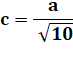|
Édition du: 06/12/2024 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
Carré découpé en huit, en dix Quelle est
l'aire de cette région du carré ? Quel est le
rayon du petit cercle central ? |
||
|
|
Sommaire de cette page >>> Carré divisé en huit >>> Carré découpé en dix |
Débutants Glossaire |
|
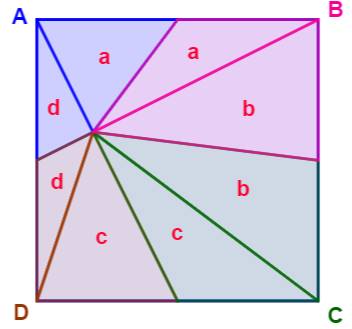
Construction Un carré et les milieux des côtés. Former les huit triangles issus d'un point
interne au carré. Connaissant les aires A, B et C des zones de la
même couleur, calculer l'aire de la zone D. Piste Les triangles de même hauteur et de bases égales
ont la même aire. C'est le cas des triangles marqués a, b, c et d. Calculs
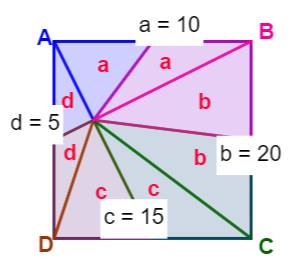
Exemple Avec a = 10, b = 20 et c = 15: D = 20 – 40 + 30 = 10 Et donc: d = 10/2 = 5 |
Exemple
|
|
|
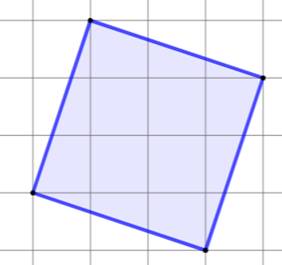
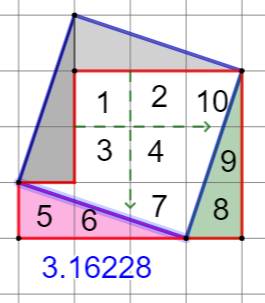
La découpe du carré Un carré dessiné sur un quadrillage. Six coups de ciseaux selon les lignes du
quadrillage produisent les pièces d'un puzzle. Assemblées ces pièces forment dix carrés égaux
(et non pas neuf). Comment est-ce possible ? Solution Les pièces non-carrées sont translatées vers la
droite ou vers le bas pour les associer et former 2 × 3 = 6 carrés identiques. En ajoutant les quatre carrés centraux
non-touchés, nous avons bien créé dix carrés
identiques en six coups de ciseaux à partir d'un grand carré initial. Calculs Si a est le
côté du carré, son aire est a² et, celle
de chacun des dix carrées est a² / 10. Longueur du côté de chaque petit carré: Exemple Si le quadrillage est unitaire, alors: |
Carré à découper
Effet du découpage
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/CarreDix.htm
|