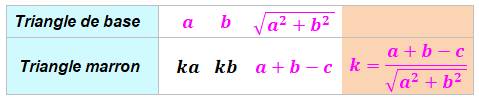Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/03/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Rectangle et deux cercles	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Carré et triangle équil.	Défis divers
	Quatre carrés	Trois cercles tangents	Trois triangles réunis
	Trois carrés plus un	Carré et rectangle	Carré divisé

Carré oblique dans grand carré Quelle est l'aire du carré interne ?
	Sommaire de cette page >>> Carré dans le grand carré >>> Carré oblique dans carré >>> Cas général	Débutants Géométrie Glossaire Géométrie

Carré dans le grand carré		haut
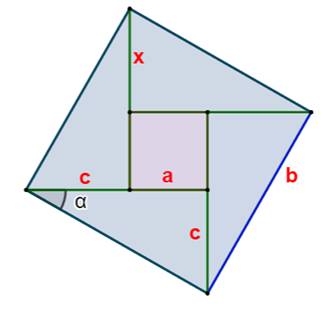
Construction Un carré central de côté a= 3cm. Quatre triangles rectangles identiques enroulés autour du carré et formant un grand carré. Leur hypoténuse vaut √89 cm. Valeur du petit côté c et de l'angle alpha ? Calculs avec le théorème de Pythagore

Carré oblique dans carré		haut
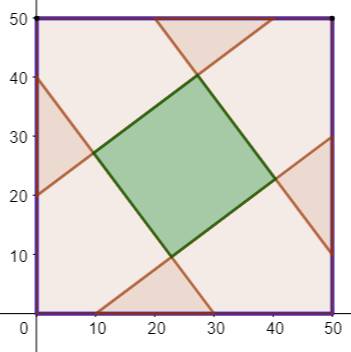
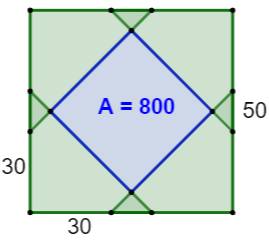
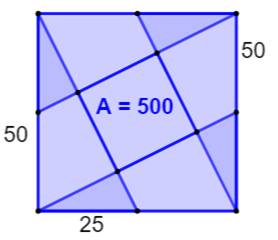
Construction Un carré de 50 cm de côté. Quatre triangles rectangle accolés aux coins du carré et de dimensions 30, 40. Quelle est l'aire du carré vert ? Solution Parallèles et symétrie permettent de démontrer que le quadrilatère vert est bine un carré. Les triangles de base sont caractéristiques: avec a = 30, b = 40, l'hypoténuse vaut: 50 (cf. théorème de Pythagore: 30² + 40² = 50²) Les triangles de base et les petits triangles marrons ont les mêmes angles deux à deux, ils sont semblables: ils ont les mêmes proportions. Les hypoténuses sont dans le rapport: 20 / 50 = 0,4. Calcul de proportions pour les autres longueurs:	Les quatre triangles (30, 40) et les quatre petits triangles marrons ont les mêmes proportions.
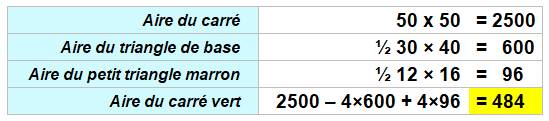
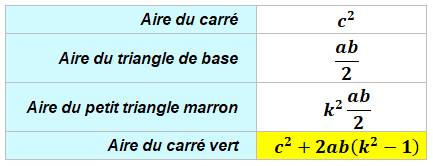
Calcul de l'aire du carré vert

D'après Mind Your Decision – Presh Talwalkar

Cas général		haut
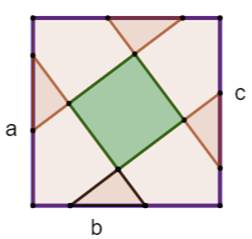
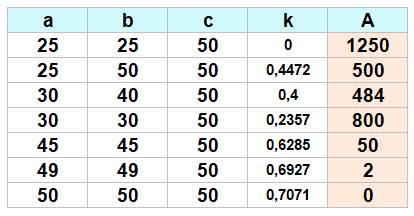
Construction Un grand carré dont le côté mesure c. Quatre triangles rectangles de mesure a et b. Quelle est l'aire du carré central vert ? Calcul du rapport d'homothétie k Calcul de l'aire du carré vert Quelques exemples	Notations Exemples

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CarObliq.htm