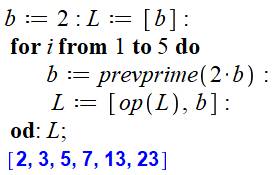type de nombres: nombres premiers de Bertrand

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/10/2025 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Premiers	NOMBRES PREMIERS				Glossaire Premiers
INDEX Types de premiers Premiers Nombres		Premiers	Presque Premiers		Probablement P.
		Premiers équilibrés	Premiers forts		Cube (cuban)
		Premiers bons	Premiers inévitables		Primeval
		Premiers de Ramanujan		Premiers de Bertrand
		Sommaire de cette page >>> Premiers entre k et 2k >>> Approche des nombres de Bertrand >>> Nombres de Bertrand >>> Généralisation en matrice >>> Programmation >>> Produit des nombres premiers

NOMBRES PREMIERS de BERTRAND

Nombres premiers se rapprochant le plus, par défaut, du double du précédent.

Anglais: Bertrand primes

Premiers entre k et 2k
Théorème de Tchebychev (ex postulat de Bertrand) Entre n et 2n, il existe toujours un nombre premier. Voir Postulat de Bertrand	Entre 100 et 200, il y a 21 nombres premiers: 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
Liste donnant la quantité de nombres premiers compris entre n et son double jusqu'à 200. Ex: n = 1 => 0, n = 10 => 4. En effet entre 10 et 20, il y a 11, 13, 17, et 19. Programme Python L = [sum(1 for k in range(n + 1, 2 * n) if isprime(k)) for n in range(1, 201)] print(L)	0, 1, 1, 2, 1, 2, 2, 2, 3, 4, 3, 4, 3, 3, 4, 5, 4, 4, 4, 4, 5, 6, 5, 6, 6, 6, 7, 7, 6, 7, 7, 7, 7, 8, 8, 9, 9, 9, 9, 10, 9, 10, 9, 9, 10, 10, 9, 9, 10, 10, 11, 12, 11, 12, 13, 13, 14, 14, 13, 13, 12, 12, 12, 13, 13, 14, 13, 13, 14, 15, 14, 14, 13, 13, 14, 15, 15, 15, 15, 15, 15, 16, 15, 16, 16, 16, 17, 17, 16, 17, 18, 18, 18, 18, 18, 19, 19, 19, 20, 21, 20, 20, 19, 19, 19, 20, 19, 19, 18, 18, 18, 19, 18, 19, 20, 20, 21, 21, 21, 22, 23, 23, 23, 23, 23, 24, 23, 23, 24, 24, 23, 24, 24, 24, 25, 26, 25, 25, 25, 25, 26, 27, 27, 27, 27, 27, 28, 28, 27, 27, 26, 26, 26, 27, 27, 28, 28, 28, 29, 29, 29, 29, 28, 28, 28, 29, 28, 28, 29, 29, 29, 29, 28, 29, 30, 30, 31, 31, 30, 31, 30, 30, 30, 31, 31, 31, 32, 32, 32, 33, 32, 33, 32, 32, 33, 33, 32, 32, 32, 32, … OEIS A060715
Liste donnant la quantité de nombres premiers compris entre p et son double, p étant un n nombre premier Ex: (11, 3) => p = 11, alors il y a trois nombres premiers entre 11 et 22. Ce sont 13, 17 et 19. Programme Python from sympy import isprime, primerange P = list(primerange(2, 542))[:100] L = [] for p in P: k = sum(1 for n in range(p + 1, 2 * p) if isprime(n)) L.append((p, k)) print(L)	(2, 1), (3, 1), (5, 1), (7, 2), (11, 3), (13, 3), (17, 4), (19, 4), (23, 5), (29, 6), (31, 7), (37, 9), (41, 9), (43, 9), (47, 9), (53, 11), (59, 13), (61, 12), (67, 13), (71, 14), (73, 13), (79, 15), (83, 15), (89, 16), (97, 19), (101, 20), (103, 19), (107, 19), (109, 18), (113, 18), (127, 23), (131, 23), (137, 25), (139, 25), (149, 27), (151, 26), (157, 28), (163, 28), (167, 28), (173, 28), (179, 30), (181, 30), (191, 32), (193, 32), (197, 32), (199, 32), (211, 35), (223, 38), (227, 38), (229, 38), (233, 39), (239, 39), (241, 39), (251, 41), (257, 42), (263, 43), (269, 42), (271, 42), (277, 42), (281, 42), (283, 42), (293, 44), (307, 49), (311, 50), (313, 49), (317, 49), (331, 54), (337, 54), (347, 56), (349, 55), (353, 55), (359, 55), (367, 57), (373, 58), (379, 59), (383, 59), (389, 60), (397, 60), (401, 60), (409, 61), (419, 64), (421, 64), (431, 66), (433, 66), (439, 66), (443, 67), (449, 67), (457, 68), (461, 68), (463, 67), (467, 67), (479, 70), (487, 71), (491, 71), (499, 73), (503, 72), (509, 73), (521, 77), (523, 76), (541, 80), … OEIS A070046

Voir Programmation – Index / Programmes Python – Index

Approche des nombres de Bertrand

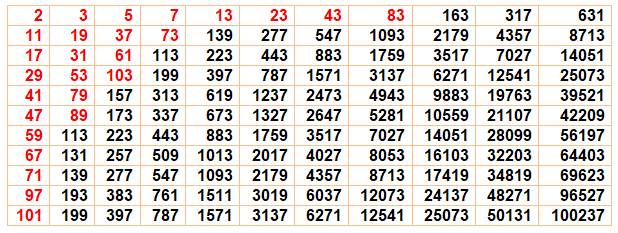
Essais

Les nombres premiers en rouge sont ceux les plus proches des doubles successifs.

Prenons 2 puis les doubles successifs

2		4		8		16		32
	3		5, 7		11, 13		17, 19, 23, 29, 31

En rouge, les nombres premiers justes inférieurs à 2^k.

Nombres de Bertrand

On reprend le même principe, mais au lieu du double du nombre précédent, on prend le double du nombre premier trouvé.

Prenons 2 puis les doubles des premiers trouvés (rouge)

2		4		6		10		14		26		46
	3		5		7		11, 13		17, 19, 23		29, 31, 37, 41, 43

En rouge, les nombres premiers de Bertrand: premier le plus proche du double du précédent nombre de Bertrand.

Le nombre 23 est un nombre premier de Bertrand, le suivant est 43, le nombre premier le plus proche de 23 x 2 = 46.

Nombres de Bertrand
Définition En commençant par B = 2, les nombres de Bertrand suivants seront les nombres premiers approchant par défaut le double du précédent nombre de Bertrand.
Liste des 50 premiers	2, 3, 5, 7, 13, 23, 43, 83, 163, 317, 631, 1259, 2503, 5003, 9973, 19937, 39869, 79699, 159389, 318751, 637499, 1274989, 2549951, 5099893, 10199767, 20399531, 40799041, 81598067, 163196129, 326392249, 652784471, 1305568919, 2611137817, 5222275627, 10444551233, 20889102457, 41778204911, 83556409789, 167112819547, 334225639093, 668451278147, 1336902556279, 2673805112521, 5347610225021, 10695220450027, 21390440900033, 42780881800057, 85561763600057, 171123527200081, 342247054400159, 684494108800091 Rang du nombre premier suivant (ex. 23, 29, 31, 37, 41, 43 Le nombre 43 est au rang 5 par rapport à 23. Liste pour les 27 plus petits: 1, 1, 1, 2, 3, 5, 9, 15, 28, 49, 90, 163, 302, 559, 1025, 1938, 3618, 6818, 12876, 24403, 46350, 88204, 168503, 321996, 617371, 1185025, 2278003, …
Liste des premiers entourant les puissances de 2 de 2 à 25 En rose: 2^k– 1est premier	[premier avant, puissance de 2, premier après] [3, 4, 5], [7, 8, 11], [13, 16, 17], [31, 32, 37], [61, 64, 67], [127, 128, 131], [251, 256, 257], [509, 512, 521], [1021, 1024, 1031], [2039, 2048, 2053], [4093, 4096, 4099], [8191, 8192, 8209], [16381, 16384, 16411], [32749, 32768, 32771], [65521, 65536, 65537], [131071, 131072, 131101], [262139, 262144, 262147], [524287, 524288, 524309], [1048573, 1048576, 1048583], [2097143, 2097152, 2097169], [4194301, 4194304, 4194319], [8388593, 8388608, 8388617], [16777213, 16777216, 16777259], [33554393, 33554432, 33554467] Même liste avec écart par rapport à la puissance de 2 [1, 4, 2], [1, 8, 4], [3, 16, 4], [1, 32, 6], [3, 64, 6], [1, 128, 4], [5, 256, 6], [3, 512, 12], [3, 1024, 10], [9, 2048, 14], [3, 4096, 6], [1, 8192, 18], [3, 16384, 30], [19, 32768, 22], [15, 65536, 16], [1, 131072, 30], [5, 262144, 8], [1, 524288, 22], [3, 1048576, 10], [9, 2097152, 26], [3, 4194304, 18], [15, 8388608, 24], [3, 16777216, 46], [39, 33554432, 74]

Généralisation en matrice

La suite des nombres de Bertrand étant établie, le plus petit nombre premier manquant (11) est utilisé pour relancer une nouvelle liste sur le même principe. Puis, le procédé est répété avec le nouveau premier manquant (17). Etc.

Matrice couvrant tous les premiers jusqu'à 100

Programmation Maple

But

Créer la liste des nombres de Bertrand

Commentaires

Initialisation du premier nombre de Bertrand: b = 2 et introduction dans la liste L.

Boucle de k itérations (ici: 5)

Calcul du nombre premier précédent 2b. Il est rangé dans la liste L.

La prochaine itération fait le même calcul avec la nouvelle valeur de b.

Voir Programmation – Index

Produit des nombres premiers
Théorème Le produit de k (k>3) nombres premiers successifs jusqu'à p est supérieur au carré du nombre premier suivant.	Exemples k = 4: 2 x 3 x 5 x 7 = 210 > 11² = 121 k = 5: 210 x 11= 2 310 > 13² = 169 k = 6: 2 310 x 13 = 30 030 > 17² = 289 etc.

Suite	Voir haut de page Repunit Nombres premiers tronquables Nombres premiers effaçables Primeval
Voir	Tables de nombres – Index Types de premiers – Index Premiers – Index Place de ces nombres parmi les autres premiers Écarts entre nombres premiers – Index Jumeaux, cousins, constellations – Index
DicoNombre	Accès aux nombres cités sur cette page
Sites	Postulat de Bertrand – Wikipédia Bertrand's Postulate – Wolfram MathWorld OEIS A006992 – Bertrand primes: a(n) is largest prime < 2a(n-1) for n > 1, with a(1) = 2 OEIS A229607 - Array: each row starts with the least prime not in a previous row, and each prime p in a row is followed by the greatest prime < 2p
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremBert.htm