|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Chiffres des PUISSANCES de 2 |
Voir Apparition des chiffres dans les puissances
de 2
|
Quelle
est la puissance de 2 qui atteint la première une quantité de chiffres en
dizaines ? |
Exemple 230
= 1073741824 => 10 chiffres |
||||||
|
30, 10 64, 20 97, 30 130, 40 163, 50 196, 60 230, 70 263, 80 296, 90 329, 100 363, 110 396, 120 429, 130 462, 140 495, 150 529, 160 562, 170 595, 180 628, 190 662, 200 695, 210 728, 220 761, 230 794, 240 828, 250 861, 260 |
894, 270 927, 280 961, 290 994, 300 1027, 310 1060, 320 1093, 330 1127, 340 1160, 350 1193, 360 1226, 370 1260, 380 1293, 390 1326, 400 1359, 410 1392, 420 1426, 430 1459, 440 1492, 450 1525, 460 1558, 470 1592, 480 1625, 490 1658, 500 1691, 510 |
1725, 520 1758, 530 1791, 540 1824, 550 1857, 560 1891, 570 1924, 580 1957, 590 1990, 600 2024, 610 2057, 620 2090, 630 2123, 640 2156, 650 2190, 660 2223, 670 2256, 680 2289, 690 2323, 700 2356, 710 2389, 720 2422, 730 2455, 740 2489, 750 2522, 760 |
2555, 770 2588, 780 2622, 790 2655, 800 2688, 810 2721, 820 2754, 830 2788, 840 2821, 850 2854, 860 2887, 870 2920, 880 2954, 890 2987, 900 3020, 910 3053, 920 3087, 930 3120, 940 3153, 950 3186, 960 3219, 970 3253, 980 3286, 990 3319, 1000 3352, 1010 |
3386, 1020 3419, 1030 3452, 1040 3485, 1050 3518, 1060 3552, 1070 3585, 1080 3618, 1090 3651, 1100 3685, 1110 3718, 1120 3751, 1130 3784, 1140 3817, 1150 3851, 1160 3884, 1170 3917, 1180 3950, 1190 3983, 1200 4017, 1210 4050, 1220 4083, 1230 4116, 1240 4150, 1250 4183, 1260 |
4216, 1270 4249, 1280 4282, 1290 4316, 1300 4349, 1310 4382, 1320 4415, 1330 4449, 1340 4482, 1350 4515, 1360 4548, 1370 4581, 1380 4615, 1390 4648, 1400 4681, 1410 4714, 1420 4748, 1430 4781, 1440 4814, 1450 4847, 1460 4880, 1470 4914, 1480 4947, 1490 4980, 1500 |
||
|
An On
|
|||||||
Les chiffres
des puissances de 2 en puissances de 6 à 15
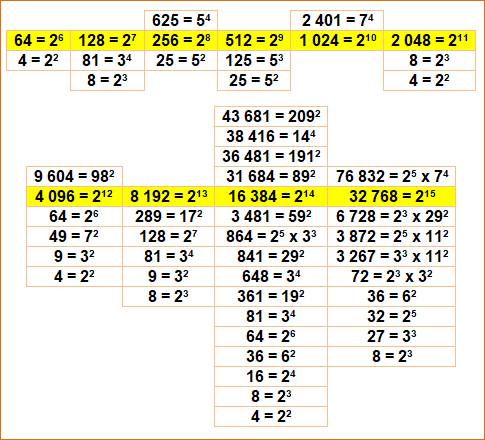
Voir Brève
637
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
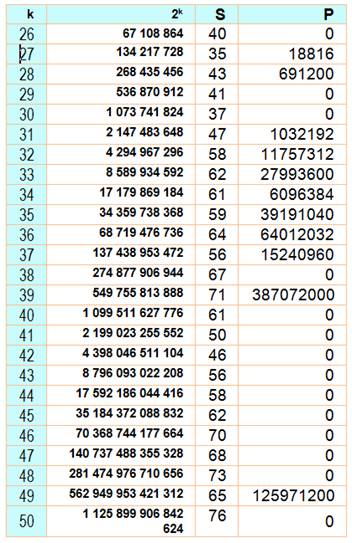
Puissance de 2 jusqu'à 50 avec identification des chiffres pairs et
des chiffres impairs Exemple: k = 10; n = 1024; 3 chiffres pairs et 1 seul
impair qui sont (0, 2, 4) et (1). En jaune, les seules puissances de 2 avec
chiffres pairs (sûr jusqu'à k = 50 000)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Record plus de
chiffres pairs
que de chiffres impairs [écart, k, n, #P, #I, chiffres pairs, chiffres impairs] |
1, 1, 2, 1, 0, [2], [] 2, 6, 64, 2, 0, [6, 4], [] 4, 11, 2048, 4, 0, [2, 0, 4, 8], [] 5, 23, 8388608, 6, 1, [8, 8, 8, 6, 0, 8], [3] 6, 66, 73786976294838206464, 13, 7, [8, 6, 6, 2, 4, 8, 8, 2, 0, 6, 4,
6, 4], [7, 3, 7, 9, 7, 9, 3] 10, 71, 2361183241434822606848, 16, 6, [2, 6, 8, 2, 4, 4, 4, 8, 2, 2,
6, 0, 6, 8, 4, 8], [3, 1, 1, 3, 1, 3] |
|
Record plus de
chiffres impairs que de chiffres pairs |
-1, 9, 512, 1, 2, [2], [5, 1] -2, 17, 131072, 2, 4, [0, 2], [1, 3, 1, 7] -3, 34, 17179869184, 4, 7, [8, 6, 8, 4], [1, 7, 1, 7, 9, 9, 1] -4, 37, 137438953472, 4, 8, [4, 8, 4, 2], [1, 3, 7, 3, 9, 5, 3, 7] -5, 40, 1099511627776, 4, 9, [0, 6, 2, 6], [1, 9, 9, 5, 1, 1, 7, 7, 7] -7, 75, 37778931862957161709568, 8, 15, [8, 8, 6, 2, 6, 0, 6, 8], [3,
7, 7, 7, 9, 3, 1, 9, 5, 7, 1, 1, 7, 9, 5] -9, 76, 75557863725914323419136, 7, 16, [8, 6, 2, 4, 2, 4, 6], [7, 5,
5, 5, 7, 3, 7, 5, 9, 1, 3, 3, 1, 9, 1, 3] |
![]()
|
PAIR / PREMIER Cas où le
nombre avec les chiffres pairs est premier
(= 2, seule possibilité). |
2, [2], 2 n , chiffres
pair, nombre avec les chiffres pairs 32, [2], 2 512, [2], 2 131072, [0, 2], 2 |
|
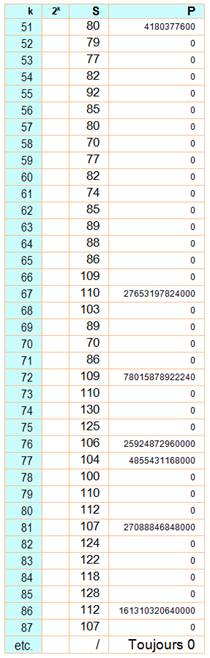
IMPAIR / PREMIER Cas où le
nombre avec les chiffres impairs est premier. Exemple: 8 192
=> 19 est premier En rose les cas
ou le nombre avec les impairs ne comporte pas plus de deux chiffres
différents. Aucun autre jusqu'à la puissance 500. |
32, [3], 3 256, [5], 5 8192, [1, 9], 19 16384, [1, 3], 13 32768, [3, 7], 37 524288, [5], 5 1048576, [1, 5, 7], 157 4194304, [1, 9, 3], 193 8388608, [3], 3 67108864, [7, 1], 71 134217728, [1, 3, 1, 7, 7], 13177 536870912, [5, 3, 7, 9, 1], 53791 2147483648, [1, 7, 3], 173 8589934592, [5, 9, 9, 3, 5, 9], 599359 68719476736, [7, 1, 9, 7, 7, 3], 719773 549755813888, [5, 9, 7, 5, 5, 1, 3], 5975513 1099511627776, [1, 9, 9, 5, 1, 1, 7, 7, 7], 199511777 4398046511104, [3, 9, 5, 1, 1, 1], 395111 8796093022208, [7, 9, 9, 3], 7993 4611686018427387904, [1, 1, 1, 7, 3, 7, 9], 1117379 4722366482869645213696, [7, 3, 9, 5, 1, 3, 9], 7395139 9444732965739290427392, [9, 7, 3, 9, 5, 7, 3, 9, 9, 7, 3, 9],
973957399739 18889465931478580854784, [1, 9, 5, 9, 3, 1, 7, 5, 5, 7], 1959317557 151115727451828646838272, [1, 5, 1, 1, 1, 5, 7, 7, 5, 1, 3, 7],
151115775137 1208925819614629174706176, [1, 9, 5, 1, 9, 1, 9, 1, 7, 7, 1, 7],
195191917717 4835703278458516698824704, [3, 5, 7, 3, 7, 5, 5, 1, 9, 7], 3573755197 |
|
IMPAIR / PREMIER Le nombre
premier impair commence par trois chiffres identiques. |
262 = 4611686018427387904 => 1117379 2118 = 332306998946228968225951765070086144 => 333999959517571 Cas suivant pour 2^824 et le nombre commence par 11177131… |
|
Note: les valeurs indiquées sont quasi-certaines, mais non prouvées. La
probabilté de trouver des valeurs nettement supérieures à celles indiquées
est très, très faible. Puissance de 2 pannumériques (qui
contiennent tous les chiffres) 251
= 2251799813685248 Plus
petite avec tous les chiffres de 1 à 9 268
= 295147905179352825856 Plus
petite avec tous les chiffres de 0 à 9 2169
= 748288838313422294120286634350736906063837462003712 à
partir de 169, toutes les puissances de 2 sont pannumériques
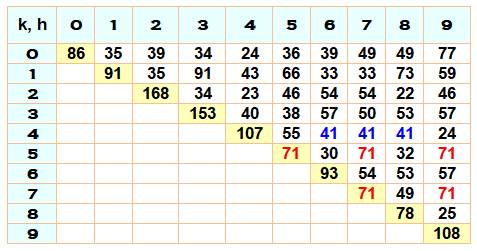
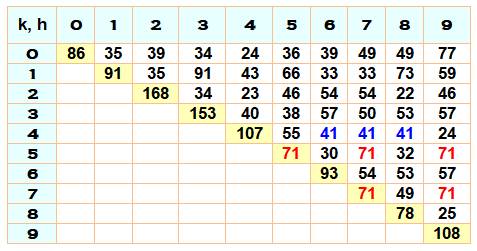
(au moins une fois tous les chiffres). Plus grande puissance sans le chiffre k [0/86, 1/91, 2/168, 3/153, 4/107,
5/71, 6/93, 7/71, 8/78, 9/108] Exemple: après la puissance 86, toutes les puissances de 2 contiennent un 0. Plus grandes puissances sans les chiffre k et h Pour k = h, on retrouve les valeurs indiquées ci-dessus. Au-delà des valeurs indiquées, la puissance de 2 comporte au moins un
chiffre k ou un chiffre h.
241 = 2 199 023 255 552: dernière puissance de 2 sans (4, 6, 7, et 8). 271 = 2 361 183 241 434 822 606 848: dernière puissance de 2
sans (5, 7 et 9) |
Voir Pi Pannumérique / Carrés et cubes pannumériques
![]()
|
Zéros dans les puissance de 2 Exposant, valeur de la puissance de 2, quantité de 0 record 10, 1024, 1 42, 4398046511104, 2 43, 8796093022208, 3 79, 604462909807314587353088, 4 88, 309485009821345068724781056, 5 100, 1267650600228229401496703205376, 6 Voir
Brève
776 |
Présence de deux mêmes chiffres consécutifs 0 => 253 = 9 007 199
254 740 992 1 => 240 = 1 099 511
627 776 2 => 243 = 8 796 093 022 208 3 => 225 = 33 554 432 4 => 218 = 262 144 5 => 216 = 65 536 6 => 246 = 70 368 744 177 664 7 => 224 = 16 777 216 8 => 219 = 524 288 9 => 233 = 8 589 934
592 Voir idem pour trois
chiffres consécutifs |
|
Liste des exposants des puissances de 2 occasionnant k
chiffres identiques de suites 2 => [53, 40, 43, 63, 18, 16, 46, 24, 19, 33] Cette liste reprend les exposants vus
ci-dessus 3 => [242, 42, 43, 83, 44, 41, 157, 24, 39, 50] 5 => [1491, 485, 314, 221, 315, 973, 220, 317, 316, 422] 6 => [1492, 1841, 2354, 2270, 3396, 973, 2269, 972, 971, 2187] |
|
|
Puissance n de 2 dans laquelle, on
retrouve une autre puissance m de 2 dans ses chiffres |
Exemple 226
= 67108864 26 = 64 |
||
|
Liste des valeurs de m pour chaque valeur de n Liste
limitée à 20 valeurs de m; exploration jusqu'à m = 100 et n = 2000 2, [6, 10, 11, 12, 14, 18, 19, 20, 22, 25, 26, 27, 28, 30, 31, 32, 33,
34, 35, 36] 3, [7, 11, 13, 14, 15, 19, 20, 23, 26, 27, 28, 29, 30, 31, 33, 34, 35,
36, 37, 38] 4, [14, 24, 40, 44, 62, 64, 70, 75, 81, 82, 84, 95, 96, 98, 99, 104,
106, 107, 109, 111] 5, [15, 25, 41, 45, 47, 65, 71, 73, 76, 82, 85, 95, 97, 100, 105, 108,
110, 112, 118, 120] 6, [26, 31, 46, 59, 66, 67, 72,
77, 83, 86, 89, 92, 96, 101, 103, 105, 106, 109, 111, 116] 7, [102, 104, 107, 192, 203, 207, 221, 248, 257, 263, 271, 279, 307,
312, 321, 322, 324, 325, 329, 331] 8, [103, 108, 146, 161,
191, 208, 222, 230, 249, 258, 260, 272, 283, 308, 309, 313, 322, 325, 332,
344] 9, [104, 109,
135, 192, 209, 221, 223, 231, 241, 259, 266, 277, 283, 285, 293, 302, 305,
309, 314, 323] 10, [224,
278, 286, 452, 473, 502, 510, 645, 656, 698, 744, 871, 889, 909, 921, 955,
960, 966, 972, 1010] 11, [103, 267, 279, 287, 404, 503, 511, 515, 657, 685, 745, 763, 883,
890, 922, 946, 973, 991, 1011, 1087] 12, [104, 268, 346, 405, 455, 462, 504, 512, 658, 726, 820, 884, 923,
947, 974, 992, 994, 1012, 1122, 1123] 13, [105, 269, 406, 463, 505, 513, 518, 536, 559, 570, 659, 821, 924,
948, 981, 993, 995, 1013, 1081, 1133] 14, [506, 571, 1082, 1166, 1409, 1489, 1601, 1630, 1686] 15, [507, 1167, 1490, 1631, 1687] 16, [452, 767, 1168, 1343, 1688, 1751, 1757, 1947] 17, [1169] 18, [1170] 19, [1171] |
|||
|
Exemple 2103 = 10141204801825835211973625643008 26
= 64 29 = 512 211 = 2048
|
|
||
![]()
|
Suite |
|
|
Autour des puissances de 2 |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()