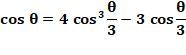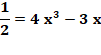Géométrie: les Problèmes impossibles de l'antiquité

Édition du: 05/03/2022

INDEX Histoire Constructions Géométrie	Histoire des maths – Antiquité
	Introduction	Duplication du cube		Trisection de l'angle
	Segment de parabole	Quadrature du cercle		Heptagone
	Historique de la quadrature		Exemples de quadratures

Faites un double-clic pour un retour en haut de page

Trois Problèmes de l'Antiquité

S'il existe encore aujourd'hui de nombreux problèmes qui résistent aux mathématiciens, dans l'Antiquité trois problèmes de géométrie avaient cette notoriété.

Après de nombreuses tentatives de recherche de solution, la sentence est tombée: on a démontré que leur résolution est impossible.

Sommaire de cette page

>>> Méthodes de construction

>>> Constructibles ?

>>> Trois ou quatre problèmes

>>> Résolutions impossibles

>>> Preuves en bref

>>> Transcendant

Débutants

Géométrie

Glossaire

Géométrie

Anglais: The three classical construction problems of antiquity are known as

Squaring the circle, Trisecting an angle, and Doubling a cube.

Méthodes de construction de Pappus			haut
Plane (2D)	En volume (3D)	Linéaire
Construction avec des droites et des cercles, dites "à la règle et au compas".	Construction avec des sections de cônes.	Construction avec des courbes plus complexes.

Constructibles ?		haut
Règle et compas Dessin d'une droite passant par deux points Dessin d'un cercle avec un point pour centre et passant par un point. On dit construction à la règle et au compas ou encore construction avec les outils euclidiens.	Recherches Il a fallu deux millénaires pour démontrer que ces trois problèmes soient déclarés insolubles. Avant comme après cette preuve, de nombreux mathématiciens amateurs ont cherché des solutions, malgré tout.
Polygones réguliers constructibles Le théorème de Gauss indique quels sont les polygones réguliers constructibles à la règle et au compas: 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, …	Figures constructibles En 1837, Wantzel (1814-1848) trouve un critère de non-constructibilité à la règle et au compas appelé théorème de Wantzel. Une longueur constructible doit être racine d'un polynôme.

Géométrie: les trois problèmes (ou quatre)

haut

Quadrature du cercle

Squaring a circle

Étant donné un cercle, construire un carré qui a exactement la même aire.

Duplication du cube

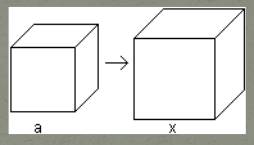
Doubling the Cube

Étant donné un cube, construire un autre cube dont le côté le volume est le double de l'original.

Trisection de l'angle

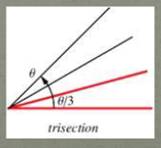
Angle trisection

Étant donné un angle, construire un autre angle dont la mesure est exactement un tiers de l'original.

Construction de l'heptagone régulier

Constructing a regular heptagon
Construire un polygone régulier à sept côtés à la règle et au compas.

Résolutions impossibles			haut
Duplication du cube. Trisection de l'angle. Construction de l'heptagone régulier. Ces trois problèmes sont de la même catégorie Il s'agit de la résolution d'équations du troisième degré Leurs racines ne sont pas constructibles.		Quadrature du cercle. Problème un peu différent, mais tout aussi impossible. L'impossibilité résulte du fait que p est transcendant, c'est-à-dire non-algébrique. L'aire du cercle de rayon 1 est p. Il n'est pas possible de construire un carré d'aire égale à p.
La démonstration de l'impossibilité n'est pas géométrique mais algébrique. Il existe deux théorèmes pertinents:	Théorème Une longueur n'est constructible avec les outils euclidiens que si elle représentée par un nombre algébrique. Théorème Une longueur est impossible à construire si elle est la racine d'une équation du troisième degré à coefficient rationnels, mais sans racines rationnelles. En résumé Un nombre constructible est algébrique, mais tous les algébriques ne sont pas constructibles.

Preuves en bref		haut
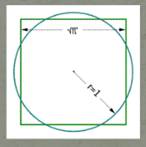
Cas de la quadrature du cercle Disque de rayon unité. Aire = π Disque de côté x. Aire x² = π	Le nombre Pi est transcendantal est donc non constructible.
Cas du cube Cube de côté unité. Aire = 1 Cube dupliqué de côté x. Aire = 2 Alors: x³ = 2	Cette équation n'a pas de racines rationnelles. Inconstructible.
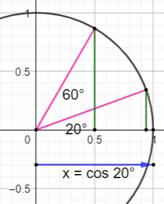
Cas de l'angle Seuls quelques angles peuvent être partagés en 3 (comme 90°). Prenons l'exemple de 60° et de l'angle tiers = 20°.	Passage à l'angle triple (ou tiers) Avec un angle de 60° et x = cos 𝛉/3 Pas de racine rationnelle donc inconstructible

Transcendant

haut

La théorie des nombres transcendantaux cherche:

les démonstrations de la transcendance ou du caractère algébrique d'un nombre, et

la possibilité d'approcher les nombres transcendants avec des nombres algébriques.

Elle permet de qualifier les racines d'une équation diophantienne et de déterminer si celle-ci possède des racines entières.

Avec cette théorie, on démontre la transcendance de la constante p.

Et, avec elle, l'impossibilité de la quadrature du cercle.

Haut de page

Retour	Exemples de quadratures
Suite	Bissection des triangles Construction de Kochansky Quadrature du carré Lunules Aire de certains croissants = aire de carrés
Voir	Équations Hilbert Histoire – Index Lunules Quadrature du triangle Quadrature de la parabole Règle et compas Transcendant
Sites	Trois grands problèmes de l'Antiquité – Wikipédia Four problems of Antiquity – Cut-the-knot The Three Famous Problems of Antiquity The complexity of geometric constructions *by François Labelle*
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Histoire/Hisantiq.htm