Divisibilité par 73, 137 et autres

Méthode par sommation de tranches de chiffres. Sujet développé sur la page divisibilités par 7, 11 et 13. La démonstration emploie la notion de congruence (modulo), en fait ni plus ni moins que les restes des divisions par 73, 137...

Divisibilité par test de congruence – Exemple137

Base: calcul des restes de la division des puissances de 10 par 137. Que l'on nomme (mod pour modulo):

Il se trouve que 73 x 137 = 10001

Ce qui conduit aux congruences indiquées dans le tableau avec des puissances en 10^4k, autrement-dit des blocs de quatre "0".

Prenons un nombre comportant 16 chiffres que nous séparons en quatre blocs de quatre chiffres: N = 10¹² A + 10⁸ B + 10⁴ C + D.

En mod 137, on remplace les puissances de 10 par la valeur en modulo 137 (tableau à droite):

Bilan: pour tester si un nombre est divisible par 137, il suffit de prendre les blocs de quatre chiffres (A, B, C, D) et de les ajouter et retrancher alternativement. Si cette somme est divisible par 137, alors le nombre d'origine l'est aussi.

Reste de la division de ces puissances de 10 par 137

Alternativement 1 et -1

Le – 1 correspond à 137 – 1 = 136

Congruence des puissances de 10 plus ou moins 1
CAS "PLUS" Si Voir Congruences et modulos	1, [11] 2, [101] 3, [7, 11, 13, 77, 91, 143] 4, [73, 137] 5, [11] 6, [101] 7, [11] 8, [17] 9, [7, 11, 13, 19, 77, 91, 133, 143, 209, 247] 10, [101]		Exemples Avec m = 137 comme avec m = 73, il faut considérer des blocs de quatre chiffres. Avec 7, 11, 13 … il suffit de former des blocs de 3 chiffes Avec 3, 9 (en bas, première ligne) aucune formation de blocs n'est nécessaire.
CAS "MOINS" Si	1, [3, 9] 2, [3, 9, 11, 33, 99] 3, [3, 9, 27, 37, 111, 333, 999] 4, [3, 9, 11, 33, 99, 101, 303, 909] 5, [3, 9, 41, 123, 271, 369, 813] 6, [3, 7, 9, 11, 13, 21, 27, 33, 37, 39, 63, 77, 91, 99, 111, 117, 143, 189, 231, 259, 273, 297, 333, 351, 407, 429, 481, 693, 777, 819, 999] 7, [3, 9, 239, 717] 8, [3, 9, 11, 33, 73, 99, 101, 137, 219, 303, 411, 657, 803,909] 9, [3, 9, 27, 37, 81, 111, 333, 999] 10, [3, 9, 11, 33, 41, 99, 123, 271, 369, 451, 813]
Liste des nombres m figurant dans ces deux listes. Avec cette méthode, on peut tester la divisibilité par les nombres de cette liste.		3, 7, 9, 11, 13, 17, 19, 21, 27, 33, 37, 39, 41, 63, 73, 77, 81, 91, 99, 101, 111, 117, 123, 133, 137, 143, 189, 209, 219, 231, 239, 247, 259, 271, 273, 297, 303, 333, 351, 369, 407, 411, 429, 451, 481, 657, 693, 717, 777, 803, 813, 819, 909, 999

Voir Méthode générale dite du domino

Divisibilité par 11

Dans le cas positif: r = 1

Première ligne dans le tableau du haut

On retrouve le critère habituel de la divisibilité par 11:

Somme alternée des chiffres: divisible par 11.

Exemple: divisibilité par 11

N =	135 795
Bloc de 1	1	3	5	7	9	5
Signe	+	–	+	–	+	–
Somme	15 – 15 = 0
Divisible ?	oui

Voir Divisibilité par 11

Divisibilité par 101

Dans le cas positif: r = 2

Deuxième ligne dans le tableau du haut

Somme alternée des blocs de deux chiffres.

Si elle est divisible par 101, le nombre d'origine l'est aussi.

Exemple: divisibilité par 101

N =	124 634
Bloc de 2	12	46	34
Signe	+	–	+
Somme	46 – 46
Divisible ?	oui

1 111 = 11 – 11 = 0

15 554 => 1 – 55 + 54 = 0

104 333 =>10 – 43 + 33 = 0

11 222 222 211 => 1 – 12 + 22 – 22 + 22 – 11 = 0

Voir Divisibilité par 101

Divisibilité par 7, 11, 13, 77, 91, 143

Dans le cas positif: r = 3

Troisième ligne dans le tableau du haut

Somme alternée des blocs de trois chiffres.

Si elle est divisible par 13, le nombre d'origine l'est aussi.

Même principe pour:
[7, 11, 13, 77, 91, 143]

Il est utile de savoir que les diviseurs de 1001 sont:
1, 7, 11, 13, 77, 91, 143, 1001.

Exemple avec 7

7 371 => 371 – 7 = 364 = 7 x 52

6 999 916 => 999 – 6 – 916 = 77 = 7 x 11

Notez qu'il suffit que la somme soit alternée. On choisit le départ qui arrange les calculs.

Exemple: divisibilité par 13

N =	44 938 257
Bloc de 3	44	938	257
Signe	+	–	+
Somme	637
Divisible ?	= 13 x 49

1144 => 144 – 1= 143 = 13 x 11

12 999 987 => 999 – 987 – 12 = 0

Exemple: divisibilité par 91

N =	314 567 799
Bloc de 3	314	567	799
Signe	+	–	+
Somme	546
Divisible ?	= 91 x 6

1 144 => 144 – 1 = 143

90 998 999 => 999 + 90 – 998 = 91

Voir Divisibilité par 91

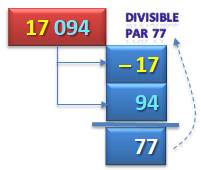
Exemple avec 77

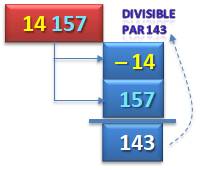
Exemple avec 143

Divisibilité par 73 et 137

Dans le cas positif: r = 4

Troisième ligne dans le tableau du haut

Somme alternée des blocs de quatre chiffres.

Si elle est divisible par 73 ou 137, le nombre d'origine l'est aussi.

Il est utile de savoir que:
73 x 137 = 1 001.

Exemple avec 73

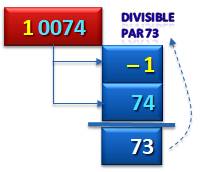
Exemple: divisibilité par 73

N =	72 098 765 433
Bloc de 4	720	9876	5433
Signe	+	–	+
Somme	3723
Divisible ?	= 73 x 51

10 074 => 74 – 1 = 73

33 434 => 3 434 – 3 = 3 431 = 73 x 47

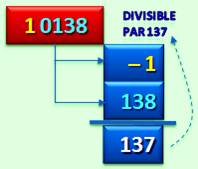
Voir Divisibilité par 73

Exemple: divisibilité par 137

N =	16 913 580 093
Bloc de 4	169	1358	0093
Signe	+	–	+
Somme	1096
Divisible ?	= 137 x 8

10 138 => 138 – 1 = 137

220 159 => 159 – 22 = 137

12 330 000 137 => 3000 – 137 – 123 = 2740 = 137 x 20

Divisibilité par 3 ou 9

Dans le cas négatif: r = 1

Première ligne dans le tableau du bas

Dans ce cas, il s'agit de l'addition des chiffres avec l'astuce de refaire la somme dès que la somme en cours dépasse 9.

On retrouve naturellement la méthode bien connue pour 3 et pour 9.

Exemple: divisibilité par 9

N =

1 370 367

Somme

1 + 3 + 7 = 11

11 + 0 + 3 + 6 = 20

2 + 7 = 9

Divisible ?

oui

Voir Divisibilité par 3 / par 9

Divisibilité par 11, 33, 99

Dans le cas négatif: r = 2

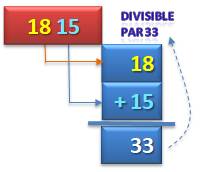
Deuxième ligne dans le tableau du bas

Dans ce cas, il s'agit de l'addition des blocs. Ce qui peut être moins intéressant que la somme alternées des chiffres de la méthode vue plus haut.

Méthode valable pour 11, 33 et 99.

Il est utile de savoir que les diviseurs de 99 sont: 1, 3, 9, 11, 33, 99.

Exemple avec 33

Exemple: divisibilité par 11

N =	135795
Bloc de 2	13	57	95
Signe	+	+	+
Somme	165
Divisible ?	165 = 15 x 11

209 => 2 + 9 = 11

77 077 => 7 + 70 + 77 = 154 = 11 x 14

Exemple avec 33:

363 => 3 + 63 = 66 = 33 x 2

264 => 2 + 64 = 66 = 33 x 2

231 033 => 23 + 10 + 33 = 66 = 33 x 2

Exemple avec 99:
198 => 1 + 98 = 99

792 =>7 + 92 = 99

700 920 => 70 + 9 + 20 = 99

Divisibilité par 27, 37, 111, 333, 999

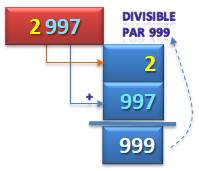
Dans le cas négatif: r = 3

Troisième ligne dans le tableau du bas

Toujours avec la somme des blocs

Méthode valable pour 27, 37, 111, 333, 999.

Il est utile de savoir que les diviseurs de 999 sont:
1, 3, 9, 27, 37, 111, 333, 999.

Exemple avec 999

Exemple: divisibilité par 27

N =	666 396 639
Bloc de 3	6	66	39	66	39
Somme	216
Divisible ?	= 27 x 8

1 026 => 1 + 26 = 27

1 404 => 1 + 404 = 405 = 27 x 15

Exemple avec 37:

1 036 => 1 + 36 = 37

3 663 => 3 + 663 = 666 = 37 x 18

328 629 856 => 328 + 629 + 856 = 1 813

et 1 813 = 37 x 49

Voir Divisibilité par 37

Exemple avec 111:
1 665 => 1 + 665 = 666 = 111 x 6

985 731 615 => 985 + 731 + 615 = 2 331

et 2 331 = 111 x 21

Exemple avec 333:
7 326 => 7 + 326 = 333

329 004 999 => 329 + 004 + 999 = 1 332

et 1 332 = 333 x 4

Exemple avec 999:
5 994 => 5 + 994 = 999

988 898 112 => 988 + 898 + 112 =1 998

et 1 998 = 999 x 2

Divisibilité par 101, 303, 909

Dans le cas négatif: r = 4

Quatrième ligne dans le tableau du bas

Notez que ce cas s'applique à [3, 9, 11, 33, 99, 101, 303, 909 mais il existe plus simple pour [3, 9, 11, 33, 99 et 101] .

Il est utile de savoir que les diviseurs de 999 sont: 1, 3, 9, 11, 33, 99, 101, 303, 909, 1111, 3333, 9999.

Exemple avec 9999

Exemple avec 101

10 0091 => 91 + 10 = 101

99 7889 8879 => 16 867 = 101 x 167

Exemple avec 303

2 9997 => 9999 => 303 x 33

299 3640 0000 => 3 939 = 303 x 13

Exemple avec 909

2 9997 => 9999 => 909 x 11

898 0920 9999 => 11 817 = 909 x 13

Suite	Divisibilité par 7 Divisibilité par 11 Divisibilité par 13 Divisibilité – Index
Voir	Calcul mental – Index Formes polynomiales Géométrie – Index Nombres abondants Nombres parfaits Théorie des nombres – Index
DicoNombre	Nombres 37, 137, 1001 et leurs curiosités Nombre 23 Nombre 73 Nombre 137 Nombre 10 001
Site	Divisibility by 7, 11 and 13 – by Alexander Bogomolny
Cette page	http://diconombre.fr/Wwwgvmm/Decompos/Div137.htm