NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths

Carrés magiques

Débutants Carrés magiques

Carré magique 6 x 6

Glossaire Carrés magiques

3x3

4x4

5x5

6x6

7x7

8x8

9x9

10x10

11x11

12x12

13x13

14x14

15x15

16x16

17x17

18x18

19x 19

20x20

INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes

Carré 6 x 6

CM 6x6 via 3x3

Premiers

Devinette

Gigogne

Soleil

Sommaire de cette page >>> Carrés magiques d'ordre 6 >>> Carrés magique 6 avec CM 3 Construction du carré d'ordre 6 >>> Méthode matricielle (De la Hire) >>> Méthode serpentin (La Loubère)

CARRÉS MAGIQUES

d'ordre 6

Somme magique: 111

Somme dans le carré: 666

Quantité de partitions* de 111: 32 134

* partitions avec les nombres de 1 à 36 tous différents

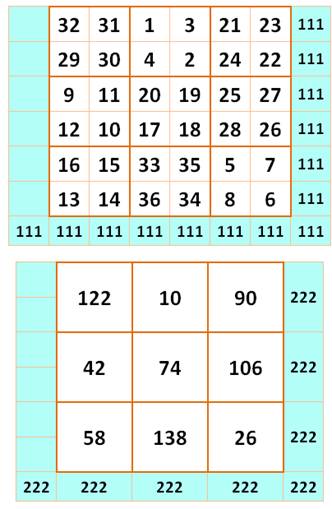
Carré magique 6x6

Chine – Yuan Dinastie (1271-1368

CARRÉ D'ORDRE 6

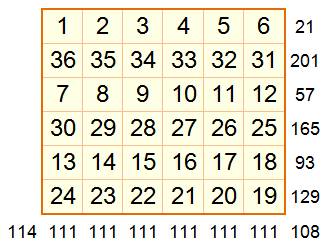
Somme magique

Nombres de 1 à 6² = 36

Somme de tous les nombres de 1 à 36 = ½ (36 x 37) = 666 !

Somme magique: 666 / 6 = 111

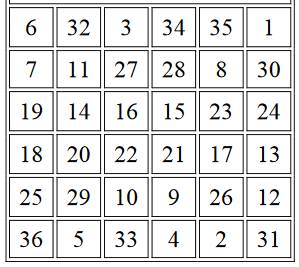
Exemple de carré magique d'ordre 6

6	25	24	13	7	36
35	11	14	20	29	2
33	27	16	22	10	3
4	28	15	21	9	34
32	8	23	17	26	5
1	12	19	18	30	31

1	32	3	34	35	6	35	3	31	8	30	4
12	29	9	10	26	25	1	32	9	28	5	36
13	14	22	21	23	18	6	7	2	33	34	29
24	20	16	15	17	19	26	21	22	17	12	13
30	11	28	27	8	7	19	23	27	10	14	18
31	5	33	4	2	36	24	25	20	15	16	11

Contrairement aux carrés d'ordre impair, les carrés d'ordre pair sont plus difficiles à construire.

Il n'existe pas de méthodes simples et universelles connues.

Carré magique 6 avec CM3
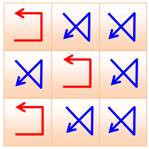
Ce carré magique d'ordre 6 est subdivisé en neuf petits carrés de quatre cellules. On calcule la somme des quatre nombres de chaque carré. Le carré 3 x 3 ainsi formé avec ces sommes est un carré magique d'ordre 3. Notez la régularité de la formation du carré d'ordre 6 par groupe de quatre nombres consécutifs, selon deux mogèles:

Construction du carré d'ordre 6 – Matrices
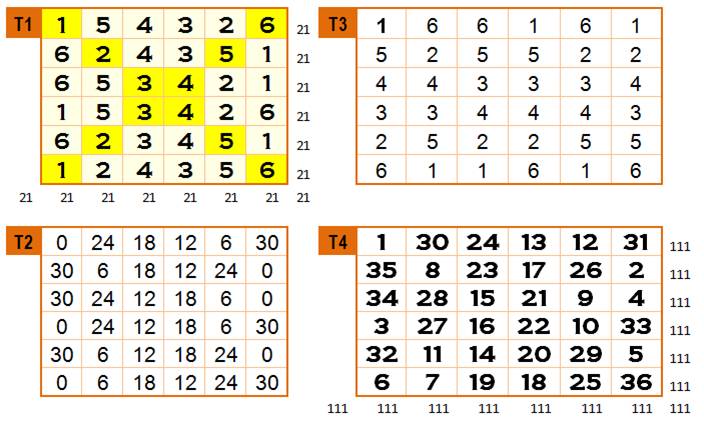
Tableau 1	Un carré latin: nombre de 1 à 6; sommes 21 sur lignes, colonnes et diagonales
Tableau 2	Tableau 1 dont chaque case est multipliée par 6 et on y retranche 6.
Tableau 3	Tableau 1 transposé: lignes deviennent colonnes. Autrement-dit, le tableau a pivoté de 90°. Résultat: les couples de nombres de cases correspondantes sont tous présents et jamais dupliqués. Carrés latins orthogonaux ou gréco-latins un peu spéciaux car les nombres sont dupliqués sur lignes et colonnes (le vrai carré gréco-latin d'ordre 6 n'existe pas)
Tableau 4	Chaque case du carré magique est la somme des cases correspondantes des tableaux 2 et 3.
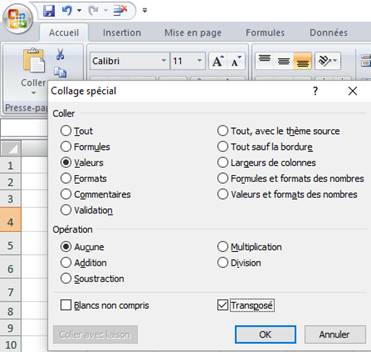
Cette disposition est pratique pour fonctionner avec un tableur. Le tableau 3 est obtenu directement en faisant: collage spécial des valeurs avec transposition (Illustration). Vous pouvez alors à loisir modifier le tableau de départ et vérifier instantanément si votre carré est magique

Voir Méthode générale / Construction du carré 8x8

Construction du carré d'ordre 6 - Serpentin
Les carrés magiques d'ordre pair ne sont pas simples à construire. Cette méthode permet de trouver la solution au prix de quelques ajustements. La première opération consiste à écrire les nombres de gauche à droite en sautant une ligne sur deux, laissant la place aux nombres écrits dans l'autre sens et en remontant.	Cette opération permet d'obtenir les sommes verticales.
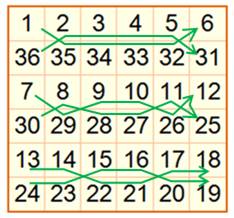
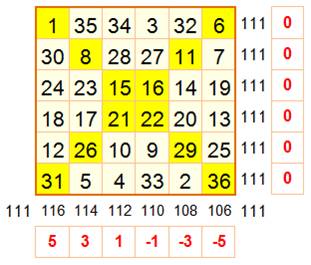
La deuxième opération consiste à créer des décalages pour satisfaire les sommes sur les lignes. Le champ est laissé libre à la créativité, pourvu que les décalages opérés sur chacun des couples de lignes soient différents. Certains passionnés ont même réalisé des tableaux qui montrent toutes les possibilités. Premier tableau: choix de trois trajets différents, doublés (lignes vertes). Il en existe beaucoup d'autres à condition de produire la somme magique sur chaque ligne verte. Deuxième tableau: les lignes sont "dépliées" selon le trajet vert choisi. Résultat: les sommes sur les lignes semblent sympathiques, mais pas correctes. Troisième tableau: avec des inversions de nombres (jaunes), les lignes présentent la même somme. Bilan: nous avons eu successivement les colonnes puis les lignes à 111. Nous sommes proches du but!
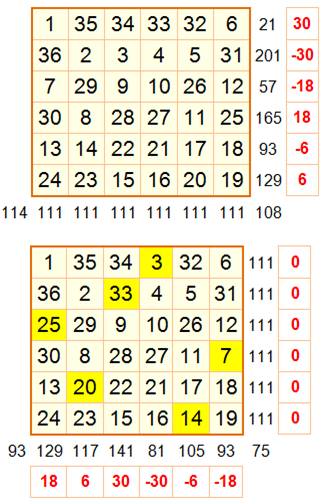
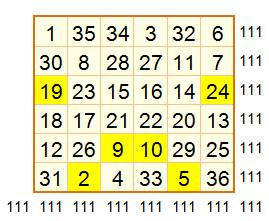
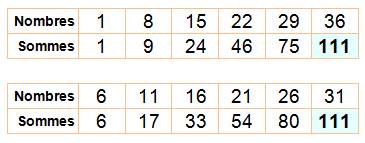
La troisième opération consiste à rétablir les sommes sur les colonnes par échanges de lignes. Intuition: progression arithmétique de 7 sur les diagonales pour passer de 1 à 36 avec les nombres 1, 8, 15, 22, 29 et 36. Même chose pour la diagonale descendante avec + 5. Premier tableau: les lignes obtenues précédemment sont déplacées pour satisfaire les nombres des diagonales. Certaines lignes sont inversées. Second tableau: quelques inversions sont réalisées pour rétablir la somme sur les colonnes, sans changer les valeurs des lignes et des diagonales. Voir Méthode générale Construction du carré 10x10	Progression arithmétique sur les diagonales

Deux autres carrés obtenus avec la même méthode

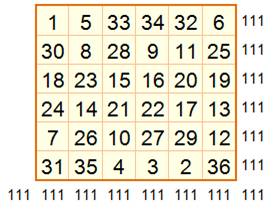
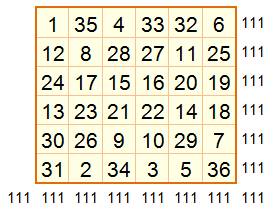
Bonus

Suite	Carré magique 6x6 à partir d'un 3x3 Carré 6x6 en devinette Carré d'ordre 7 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Énigmes Jeux Nombres en chiffres Nombres magiques - Index Rubriques débutants Sudoku
Diconombre	Nombre 6 Nombre 36 Nombre 111 Nombre 666
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordre6.htm

Renvois de liens

CARRÉ D'ORDRE 7 >>>

Avec des nombres premiers >>>

CARRÉ MAGIQUE D'ORDRE 8 >>>

Carré magique de Benjamin Franklin, ordre 8 >>>

CARRÉ D'ORDRE 9 >>>

CARRÉ D'ORDRE 10 ET PLUS >>>

AUTRES >>>