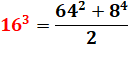|
Édition du: 05/07/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Nombre 16 |
Culture 16 |
Maths 16 |
|
|
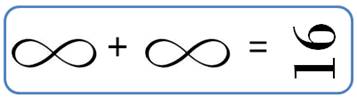
Expression
16 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
|
|||
|
Caractérisation
du nombre
|
|
Voir |
|
Rappel Propriétés générales >>>
|
16
c'est très étroit ! 16 = 13 + 3 |
|
|
Voir
Pensées
& humour / Alphabet parlant
/ Calembours
|
|
||||
|
Base du système hexadécimal. |
||||
|
|
||||
|
|
||||
|
|
||||
|
Périmètre
d'un même carré (4 + 4 + 4 + 4). |
||||
|
|
|
|||
|
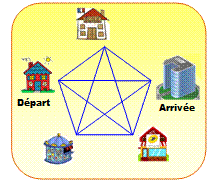
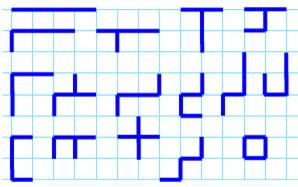
passent par trois
points exactement sur une grille régulière
de 5x5. Il y en a 32 passant par trois
points ou plus. |
|
|||
|
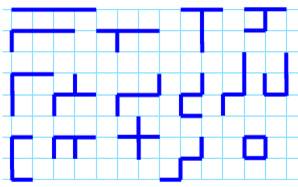
Lignes rectilignes formées de quatre
segments identiques |
|
Tetrahex |
||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
![]()
Chiffres et numération
|
16 + 61 = 77 61 – 16 = 45 = T9 |
|
||||
|
16
= (4+1) + (4–1) + (4x1) + (4/1) = (3+3) + (3–3) + (3x3) + (3/3) |
|
||||
|
16 = (1+1) × (6+2)
|
Liste: 16,
27, 396, 117 729 612 000, … |
||||
|
1 6 |
|
||||
|
|
|
||||
|
|
|
||||
|
p(16) = 231 |
|
|
16
= 1 + 3 + 5 + 7 |
|
|
16
= 1 + 3 + 5 + 7 = 16 et 1 + 6 = 7 |
Voir racine
numérique. |
|
16
+ 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24 |
|
|
16
= 7 + 9 = 1 + 2 + 3 + 4 + 6 |
Partition unique avec cinq chiffres différents. |
|
16
= 3 + 13 = 5 + 11 = 2 + 3 + 11 |
|
|
16 =
T3 + T4 = 6 + 10 |
|
|
16
= 1 + 1 + 2 + 4 + 8 |
|
|
1
+ 15 = 6 + 10 |
|
|
16
= n + (n+1) + … |
|
|
16
– 1 = 1 + 2 + 4 + 8 = 15 |
|
Multiplication, division, diviseurs
|
|
|
|
|
|
|
|
|
|
16 = |
|
|
15, [16, 28] 16 = 24 et 17 = 17 => 17 –
2 = 15 |
Seul 28
partage cette propriété (n au moins jusqu'à 109). |
|
Pour k |
|
|
16 |
|
|
dn(16) = 2 × 16
|
Liste: 16, 108, 729, 12500, 84375… |
Avec les puissances
|
16 = 2 x 2 x 2 x 2 = 24 = 4 x 4 = 42 = 22
x 22 |
Seul cas où ab = ba |
|
16 = 24 = 246 |
|
|
|
|
|
16
= 24 = 4² |
|
||
|
16
= 4² |
|
||
|
16 =
22 x 22 |
|
||
|
|
|
||
|
16
= 2² + 2² + 2² + 2² 16
= 1² + 1² + 1² + 2² + 3² |
|
||
|
16
= 23 + 23 |
|
||
|
16
= 24 |
|
||
|
16 =
21 + 32 + 51 = 23 + 31
+ 51 |
|
||
|
16
= (2² + 2²)(1² + 1²) = (4² + 0²) |
|||
|
16
= 5² – 3² |
|||
|
16 = 143 – 123 – 103 |
|
||
|
16 = 25 –
24 |
|
||
|
16 = 25 – 42 = 122 – 27 |
|||
|
16
=
2 x 2² + 8 x 1² = 3 x 2² +
4 x 1² = 1 x 2² +
3 x 2² = 2 x 2² +
2 x 2² = 1 x 23
+ 8 x 13 = 1 x 23
+ 1 x 23 = 1 x 32
+ 7 x 12 |
Carrés et autres puissances. |
||
|
16
= 5/2 (2² + 2) + 1 |
|
||
|
16
= 21,821 . 22,179 16
= 2 a . 2 b |
Voir Exposants |
||
|
16 = (1 + i)8 = (1 – i)8 = (1 + i)7 + (1 – i)7 –16 = ( |
|
||
|
16 |
|
||
|
16² =
8² + 8² + 8² + 8² |
|
||||
|
162 = 1² + 2² + 7² + 9² + 11² = 1² + 3² + 5² + 10² + 11² = 1² + 5² + 7²+ 9² + 10² = 2² + 3² + 5² + 7² + 13² |
|
||||
|
16²
= 256 & 2 + 5 + 6 = 13 132 = 169 &
1 + 6 + 9 = 16 |
|
||||
|
|
Voir Nombre 162 pour P4, moyenne de P3 et P5. |
||||
|
|
|||||
|
|
|
||||
|
166 = 16 777216 |
|
||||
|
|
Voir Nombre
499499 |
||||
Dénombrement, jeux et curiosités
|
16 = ½ (5 x 6) + 1 |
|
|
|
16 = 1/3 x 4(4² – 3x4
+ 8) |
|
|
|
16 = Qe(5) |
|
|
|
|
|
|
Autour du nombre
|
16 & 1123 1+6 = 1+1+2+3 & 1x6= 1x1x2x3 |
|
|
1 / 16,335 = 0,06 12 18 … |
|
|
|
|
|
16 [123, 234, 345,
456, 567, 678, 789] [135, 246, 357,
468, 579] [147, 258, 369] [159] |
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 0, 0, 0] 3, [1, 2, 1] 4, [1, 0, 0] 5,
[3, 1] 6,
[2, 4] |
7, [2, 2] 8,
[2, 0] 9,
[1, 7] 10,
[1, 6] 11,
[1, 5] |
12,
[1, 4] 13,
[1, 3] 14,
[1, 2] 15, [1, 1] 16,
[1, 0] |
7,
[2, 2] 15,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
![]()