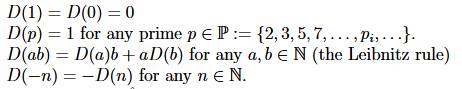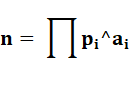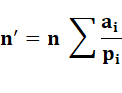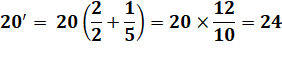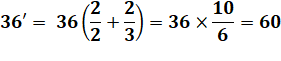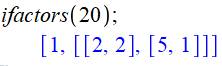Dérivée numérique

Édition du: 04/04/2025

INDEX Analyse	Analyse – Dérivée
	Approche	Historique	Débutants	Développement
	Ficelles de première		Approche en première	Les dérivées
	Intérêt des dérivées		Exemples résolus	Exemples (limites)
	Dérivée numérique

Faites un double-clic pour un retour en haut de page

DÉRIVÉE NUMÉRIQUE

On sait dériver les fonctions. Mais, sait-on dériver des nombres? Oui, en utilisant la factorisation des nombres. Technique proposée en 1911 par le mathématicien espagnol Josè Mingot Shelly.

À quoi cela sert-il ? Un autre outil à la disposition des chercheurs en théorie des nombres. Notamment pour résoudre des conjectures qui résistent encore.

Sommaire de cette page

>>> Approche

>>> Définition et Intérêt

>>> Calculs

>>> Calcul détaillé pour 360

>>> Table

>>> Jamais dérivée numérique

>>> Dérivées seconde, tierce … Table

>>> Graphe des dérivées numériques (0 à 499)

>>> Records

>>> Retournement

Débutants

Nombres

Glossaire

Nombres

Anglais: Arithmetic derivative or number derivative

Approche

haut

Quelques cas typiques

Nombres premiers: leur dérivée est égale à 1.

Nombres semi-premiers (deux facteurs): leur dérivée est égale à la somme des deux facteurs

Exemples

7 = 1 × 7 => 7' = 1

15 = 3 × 5 => 15' = 3 + 5 = 8

4 = 2 × 2 => 4' = 2 + 2 = 4

Règles de construction

Deux règles:

Pour tout premier p, p' = 1; et

Pour tout composé n = ab, n' = ab' + a'b

La dérivée d'un nombre négatif est l'opposé de la dérivée de a valeur positive. (-n)' = -n'

Cas de 1

1 = 1 × 1 => 1' = 1 × 1' + 1' × 1

= 2 × 1'

Seule possibilité pour satisfaire cette égalité:

1' = 0

Cas de 0

0 = 0 × 1 => 0' = 0 × 1' + 1' × 0 = 0

Règle de dérivation d'un produit à deux facteurs

Soit un nombre n composé égal au produit a∙b, sa dérivée est égale à:

n = a ∙ b

= > n' = a ∙ b' + a' ∙ b

Cette formule est connue sous le nom de règle de Leibniz relative à la différenciation des produits:

(f(x).g(x))' = f'(x).g(x) + f(x).g'(x)

Exemples

20 = 4 × 5 => 20' = 4 × 5' + 4' × 5

= 4 × 1 + 4 × 5 = 24

40 = 2 × 20 => 40' = 2 × 20' + 2' × 20

= 2 × 24 + 1 × 20 = 68

Règle de dérivation d'un produit à trois facteurs

n = a ∙ b ∙ c

= > n' = (a ∙ b) c' + (a ∙ b)' c

n' = a ∙ b ∙ c' + (a ∙ b' + a' ∙ b) c

n' = a ∙ b ∙ c' + a ∙ b' ∙ c + a' ∙ b ∙ c

Pour les puissances, on retrouve la règle habituelle:
(n^k)' = k × n' × n^{k – 1}

Exemples

30 = 2 × 3 × 5

=> 30' = 2×3×1 + 2×1×5 + 1×3×5

= 6 + 10 + 15 = 31

216 = 6 × 6 × 6 = 6³

=> 216' = 6×6×5 + 6×5×6 + 5×6×6

= 3 × 6×6×5 = 540

ou selon la formule des puissances:

(6³)' = 3 × 5 × 6² = 540

Voir Brève 62-1227

Définition et Intérêt

La dérivée d'un entier est l'application donnant une image à tout nombre:

la valeur 1 aux nombres premiers, et

satisfaisant la règle de Leibniz pour tous les autres.

The derivative of an integer to be the map sending every prime to 1 and satisfying the Leibniz rule.

Les quatre règles & extension aux nombres rationnels

La dérivation des nombres est un outil mathématique utile en théorie des nombres.

Elle permet d'aborder sous un angle nouveau

la conjecture de Goldbach
Pour k>1, il existe un nombre n tel que n' = 2k

la conjecture des nombres premiers jumeaux
S'il existe une infinité de jumeaux, alors il existe une infinité de k tels que k'' = 1

Calcul		haut
Formule	Exemples
Programme Maple	But Lister la valeur de la dérivée numérique des nombres de 0 à 100. Commentaires Effacement de toute donnée antérieure (restart). Appel des programmes de théorie des nombres. Mise en place d'une procédure (un sous-programme). Déclaration des variables internes à la procédure (local). Calcul en F des facteurs de n sous la forme Sélection de la deuxième suite avec [2]. Calcul de la formule en balayant tous les facteurs F[i,1] et leur puissance F[i,2]. Calcul final en multipliant cette somme s par n. Le programme principal demande d'imprimer n et sa dérivée pour les nombres de 0 à 100.

Calcul détaillé pour 360

Vers la droite: décomposition en deux facteurs

Vers la gauche: calcul progressif de la formule

Table des dérivées numériques de 0 à 499

haut

0, 0

1, 0

2, 1

3, 1

4, 4

5, 1

6, 5

7, 1

8, 12

9, 6

10, 7

11, 1

12, 16

13, 1

14, 9

15, 8

16, 32

17, 1

18, 21

19, 1

20, 24

21, 10

22, 13

23, 1

24, 44

25, 10

26, 15

27, 27

28, 32

29, 1

30, 31

31, 1

32, 80

33, 14

34, 19

35, 12

36, 60

37, 1

38, 21

39, 16

40, 68

41, 1

42, 41

43, 1

44, 48

45, 39

46, 25

47, 1

48, 112

49, 14

50, 45

51, 20

52, 56

53, 1

54, 81

55, 16

56, 92

57, 22

58, 31

59, 1

60, 92

61, 1

62, 33

63, 51

64, 192

65, 18

66, 61

67, 1

68, 72

69, 26

70, 59

71, 1

72, 156

73, 1

74, 39

75, 55

76, 80

77, 18

78, 71

79, 1

80, 176

81, 108

82, 43

83, 1

84, 124

85, 22

86, 45

87, 32

88, 140

89, 1

90, 123

91, 20

92, 96

93, 34

94, 49

95, 24

96, 272

97, 1

98, 77

99, 75

100, 140

101, 1

102, 91

103, 1

104, 164

105, 71

106, 55

107, 1

108, 216

109, 1

110, 87

111, 40

112, 240

113, 1

114, 101

115, 28

116, 120

117, 87

118, 61

119, 24

120, 244

121, 22

122, 63

123, 44

124, 128

125, 75

126, 165

127, 1

128, 448

129, 46

130, 101

131, 1

132, 188

133, 26

134, 69

135, 162

136, 212

137, 1

138, 121

139, 1

140, 188

141, 50

142, 73

143, 24

144, 384

145, 34

146, 75

147, 91

148, 152

149, 1

150, 185

151, 1

152, 236

153, 111

154, 113

155, 36

156, 220

157, 1

158, 81

159, 56

160, 432

161, 30

162, 297

163, 1

164, 168

165, 103

166, 85

167, 1

168, 332

169, 26

170, 129

171, 123

172, 176

173, 1

174, 151

175, 95

176, 368

177, 62

178, 91

179, 1

180, 336

181, 1

182, 131

183, 64

184, 284

185, 42

186, 161

187, 28

188, 192

189, 216

190, 143

191, 1

192, 640

193, 1

194, 99

195, 119

196, 252

197, 1

198, 249

199, 1

200, 380

201, 70

202, 103

203, 36

204, 284

205, 46

206, 105

207, 147

208, 432

209, 30

210, 247

211, 1

212, 216

213, 74

214, 109

215, 48

216, 540

217, 38

218, 111

219, 76

220, 284

221, 30

222, 191

223, 1

224, 592

225, 240

226, 115

227, 1

228, 316

229, 1

230, 171

231, 131

232, 356

233, 1

234, 291

235, 52

236, 240

237, 82

238, 167

239, 1

240, 608

241, 1

242, 165

243, 405

244, 248

245, 119

246, 211

247, 32

248, 380

249, 86

250, 275

251, 1

252, 456

253, 34

254, 129

255, 151

256, 1024

257, 1

258, 221

259, 44

260, 332

261, 183

262, 133

263, 1

264, 508

265, 58

266, 185

267, 92

268, 272

269, 1

270, 459

271, 1

272, 560

273, 151

274, 139

275, 135

276, 380

277, 1

278, 141

279, 195

280, 516

281, 1

282, 241

283, 1

284, 288

285, 167

286, 191

287, 48

288, 912

289, 34

290, 213

291, 100

292, 296

293, 1

294, 329

295, 64

296, 452

297, 324

298, 151

299, 36

300, 520

301, 50

302, 153

303, 104

304, 624

305, 66

306, 375

307, 1

308, 380

309, 106

310, 227

311, 1

312, 596

313, 1

314, 159

315, 318

316, 320

317, 1

318, 271

319, 40

320, 1024

321, 110

322, 221

323, 36

324, 756

325, 155

326, 165

327, 112

328, 500

329, 54

330, 371

331, 1

332, 336

333, 231

334, 169

335, 72

336, 832

337, 1

338, 221

339, 116

340, 428

341, 42

342, 417

343, 147

344, 524

345, 199

346, 175

347, 1

348, 476

349, 1

350, 365

351, 378

352, 912

353, 1

354, 301

355, 76

356, 360

357, 191

358, 181

359, 1

360, 852

361, 38

362, 183

363, 187

364, 444

365, 78

366, 311

367, 1

368, 752

369, 255

370, 269

371, 60

372, 508

373, 1

374, 243

375, 350

376, 572

377, 42

378, 621

379, 1

380, 476

381, 130

382, 193

383, 1

384, 1472

385, 167

386, 195

387, 267

388, 392

389, 1

390, 433

391, 40

392, 700

393, 134

394, 199

395, 84

396, 696

397, 1

398, 201

399, 211

400, 960

401, 1

402, 341

403, 44

404, 408

405, 621

406, 275

407, 48

408, 772

409, 1

410, 297

411, 140

412, 416

413, 66

414, 501

415, 88

416, 1072

417, 142

418, 269

419, 1

420, 704

421, 1

422, 213

423, 291

424, 644

425, 195

426, 361

427, 68

428, 432

429, 215

430, 311

431, 1

432, 1296

433, 1

434, 293

435, 247

436, 440

437, 42

438, 371

439, 1

440, 788

441, 420

442, 281

443, 1

444, 604

445, 94

446, 225

447, 152

448, 1408

449, 1

450, 705

451, 52

452, 456

453, 154

454, 229

455, 191

456, 860

457, 1

458, 231

459, 486

460, 572

461, 1

462, 493

463, 1

464, 944

465, 263

466, 235

467, 1

468, 816

469, 74

470, 339

471, 160

472, 716

473, 54

474, 401

475, 215

476, 572

477, 327

478, 241

479, 1

480, 1456

481, 50

482, 243

483, 251

484, 572

485, 102

486, 1053

487, 1

488, 740

489, 166

490, 483

491, 1

492, 668

493, 46

494, 311

495, 474

496, 1008

497, 78

498, 421

499, 1

La dérivée numérique de 500 est 800

Jamais dérivée numérique

Certains nombres ne sont pas atteints par la dérivée numérique.

Liste pour n jusqu'à 1000:

2, 3, 11, 17, 23, 29, 35, 37, 47, 53, 57, 65, 67, 79, 83, 89, 93, 97, 107, 117, 125, 127, 137, 145, 149, 157, 163, 173, 177, 179, 189, 197, 205, 207, 209, 217, 219, 223, 233, 237, 245, 257, 261, 277, 289, 303, 305, 307, 317, 323, 325, 337, 345, 353, 367, 373, 377, 379, 387, 389, 393, 397, 409, 413, 415, 427, 429, 443, 449, 453, 457, 473, 477, 485, 497, 499, 509, 513, 515, 517, 529, 531, 533, 537, 547, 553, 561, 569, 577, 593, 597, 605, 613, 625, 629, 639, 657, 659, 665, 673, 677, 681, 683, 697, 699, 709, 713, 715, 733, 747, 749, 757, 765, 769, 777, 781, 783, 785, 787, 793, 797, 805, 809, 817, 819, 827, 833, 835, 845, 847, 849, 853, 857, 869, 873, 877, 881, 891, 895, 897, 907, 917, 925, 933, 937, 947, 953, 963, 965, 967, 981, 989, 997, …

Dérivées seconde, tierce … TABLE

Cas du nombre 100 (exemple)

Par simple lecture sur la table, on déduira les premières dérivées successives du nombre 100. Sa dérivée seconde est 140. Puis 188 / 192 / 640 / … Et, le calcul donne les suivantes: 2368 / 2352 / …

Table des dérivées successives pour n de 1 à 100

[1, 0]

[2, 1, 0]

[3, 1, 0]

[4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4]

[5, 1, 0]

[6, 5, 1, 0]

[7, 1, 0]

[8, 12, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592]

[9, 6, 5, 1, 0]

[10, 7, 1, 0]

[11, 1, 0]

[12, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592, 20096]

[13, 1, 0]

[14, 9, 6, 5, 1, 0]

[15, 8, 12, 16, 32, 80, 176, 368, 752, 1520, 3424]

[16, 32, 80, 176, 368, 752, 1520, 3424, 8592, 20096, 70464]

[17, 1, 0]

[18, 21, 10, 7, 1, 0]

[19, 1, 0]

[20, 24, 44, 48, 112, 240, 608, 1552, 3120, 8144, 16304]

[21, 10, 7, 1, 0]

[22, 13, 1, 0]

[23, 1, 0]

[24, 44, 48, 112, 240, 608, 1552, 3120, 8144, 16304, 32624]

[25, 10, 7, 1, 0]

[26, 15, 8, 12, 16, 32, 80, 176, 368, 752, 1520]

[27, 27, 27, 27, 27, 27, 27, 27, 27, 27, 27]

[28, 32, 80, 176, 368, 752, 1520, 3424, 8592, 20096, 70464]

[29, 1, 0]

[30, 31, 1, 0]

[31, 1, 0]

[32, 80, 176, 368, 752, 1520, 3424, 8592, 20096, 70464, 235072]

[33, 14, 9, 6, 5, 1, 0]

[34, 19, 1, 0]

[35, 12, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592]

[36, 60, 92, 96, 272, 560, 1312, 3312, 8976, 22288, 47872]

[37, 1, 0]

[38, 21, 10, 7, 1, 0]

[39, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592, 20096]

[40, 68, 72, 156, 220, 284, 288, 912, 2176, 7744, 24640]

[41, 1, 0]

[42, 41, 1, 0]

[43, 1, 0]

[44, 48, 112, 240, 608, 1552, 3120, 8144, 16304, 32624, 65264]

[45, 39, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592]

[46, 25, 10, 7, 1, 0]

[47, 1, 0]

[48, 112, 240, 608, 1552, 3120, 8144, 16304, 32624, 65264, 130544]

[49, 14, 9, 6, 5, 1, 0]

[50, 45, 39, 16, 32, 80, 176, 368, 752, 1520, 3424]

[51, 20, 24, 44, 48, 112, 240, 608, 1552, 3120, 8144]

[52, 56, 92, 96, 272, 560, 1312, 3312, 8976, 22288, 47872]

[53, 1, 0]

[54, 81, 108, 216, 540, 1188, 2484, 5076, 10260, 23112, 57996]

[55, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592, 20096]

[56, 92, 96, 272, 560, 1312, 3312, 8976, 22288, 47872, 198656]

[57, 22, 13, 1, 0]

[58, 31, 1, 0]

[59, 1, 0]

[60, 92, 96, 272, 560, 1312, 3312, 8976, 22288, 47872, 198656]

[61, 1, 0]

[62, 33, 14, 9, 6, 5, 1, 0]

[63, 51, 20, 24, 44, 48, 112, 240, 608, 1552, 3120]

[64, 192, 640, 2368, 7168, 36864, 245760, 1851392, 12976128, 120127488, 1012858880]

[65, 18, 21, 10, 7, 1, 0]

[66, 61, 1, 0]

[67, 1, 0]

[68, 72, 156, 220, 284, 288, 912, 2176, 7744, 24640, 84608]

[69, 26, 15, 8, 12, 16, 32, 80, 176, 368, 752]

[70, 59, 1, 0]

[71, 1, 0]

[72, 156, 220, 284, 288, 912, 2176, 7744, 24640, 84608, 296256]

[73, 1, 0]

[74, 39, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592]

[75, 55, 16, 32, 80, 176, 368, 752, 1520, 3424, 8592]

[76, 80, 176, 368, 752, 1520, 3424, 8592, 20096, 70464, 235072]

[77, 18, 21, 10, 7, 1, 0]

[78, 71, 1, 0]

[79, 1, 0]

[80, 176, 368, 752, 1520, 3424, 8592, 20096, 70464, 235072, 705280]

[81, 108, 216, 540, 1188, 2484, 5076, 10260, 23112, 57996, 135648]

[82, 43, 1, 0]

[83, 1, 0]

[84, 124, 128, 448, 1408, 5056, 15232, 56384, 169216, 677120, 2902784]

[85, 22, 13, 1, 0]

[86, 45, 39, 16, 32, 80, 176, 368, 752, 1520, 3424]

[87, 32, 80, 176, 368, 752, 1520, 3424, 8592, 20096, 70464]

[88, 140, 188, 192, 640, 2368, 7168, 36864, 245760, 1851392, 12976128]

[89, 1, 0]

[90, 123, 44, 48, 112, 240, 608, 1552, 3120, 8144, 16304]

[91, 20, 24, 44, 48, 112, 240, 608, 1552, 3120, 8144]

[92, 96, 272, 560, 1312, 3312, 8976, 22288, 47872, 198656, 1094656]

[93, 34, 19, 1, 0]

[94, 49, 14, 9, 6, 5, 1, 0]

[95, 24, 44, 48, 112, 240, 608, 1552, 3120, 8144, 16304]

[96, 272, 560, 1312, 3312, 8976, 22288, 47872, 198656, 1094656, 5474304]

[97, 1, 0]

[98, 77, 18, 21, 10, 7, 1, 0]

[99, 75, 55, 16, 32, 80, 176, 368, 752, 1520, 3424]

[100, 140, 188, 192, 640, 2368, 7168, 36864, 245760, 1851392, 12976128]

Pour information la centième dérivée du nombre 8 est supérieure à 10¹⁰⁰.

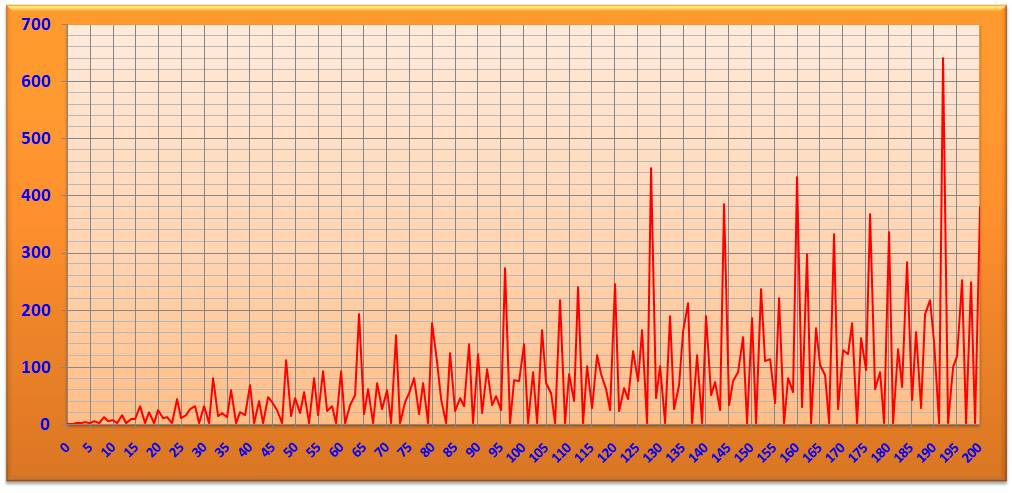
Graphe des dérivées numériques des nombres de 0 à 200

Records jusqu'à 100 000

haut

2, 1

4, 4

6, 5

8, 12

12, 16

16, 32

24, 44

32, 80

48, 112

64, 192

96, 272

128, 448

192, 640

256, 1024

384, 1472

512, 2304

640, 2368

768, 3328

960, 3392

1024, 5120

1280, 5376

1536, 7424

1920, 7744

2048, 11264

2560, 12032

3072, 16384

3584, 16640

3840, 17408

4096, 24576

5120, 26624

6144, 35840

7168, 36864

7680, 38656

8192, 53248

10240, 58368

12288, 77824

14336, 80896

15360, 84992

16384, 114688

20480, 126976

24576, 167936

28672, 176128

30720, 185344

32768, 245760

40960, 274432

49152, 360448

57344, 380928

61440, 401408

65536, 524288

73728, 528384

81920, 589824

90112, 593920

98304, 770048

Retournement

dn(366)

= dn(663) = 311

Le nombre et son retourné ont la même dérivée numérique. Plus petit cas. On exclut les nombres premiers et les nombres palindromes.

Liste: 366, 663, 3245, 3685, 5423, 5863, 8178, 8718, 14269, 15167, 16237, 18449, 18977, 36679, 73261, 76151, 77981, 94481, 96241, 97663, 140941, 149041, 150251, 152051, 196891, 198691, 302363, 308459, 319853, 335148, 358913, 363203, 841533, 921239, 932129, 954803, 958099, 990859, … OEIS A259077

Haut de page (ou double-clic)

Retour	Dérivée – Approche Règle de Leibniz
Suite	Un exercice d'approche des dérivées Approche des dérivées via le carré ou le cube des nombres Dérivées Intégrale – Approche avec 1/x Primitive Calcul de pentes
Voir	Dérivées – Glossaire Équations différentielles – Glossaire Infinitésimaux Vitesse – Glossaire
Sites	Dérivée arithmétique – Wikipédia Arithmetic derivative – Planetmath Arithmetic derivative – Rosetta Code Arithmetic derivative – Wikipedia How to differentaite à number – Victor Ufnarovski Investigations on the properties of the arithmetic derivative - Niklas Dahl, Jonas Olsson, Alexander Loiko *OEIS A003415 - a(n) = n' = arithmetic derivative of n: a(0) = a(1) = 0, a(prime) = 1, a(mn) = ma(n) + na(m). OEIS – Arithmetic derivative – Toutes les listes de nombres relatives à la dérivée numérique**
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/AnaDerNu.htm