NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/11/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	OBJETS 3D
Débutants Géométrie	CÔNE de RÉVOLUTION				Glossaire Géométrie
INDEX Géométrie	Présentation	Calculs – Cône	Calculs – Tronc de Cône	Équations
			Cône elliptique
		Sommaire de cette page >>> Volume de jus de fruit dans verre conique >>> Volume du cône de crème glacée >>> Cône maximum >>> Patron du cône

Cônes – Calculs

Quelques exercices qui montrent comment calculer le volume du cône.

Le premier exemple montre un calcul pas à pas de niveau collège.

Volume de jus de fruit dans verre conique
Verre conique dans lequel on verse un jus de fruit à une certaine hauteur. La figure donne les paramètres.	Quel est le volume en centilitre du jus de fruit dans le verre?

Voir Théorème de Pythagore / Théorème de Thalès

VOLUME du CÔNE de crème glacées
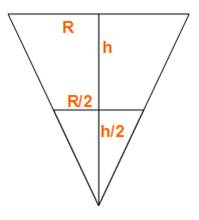
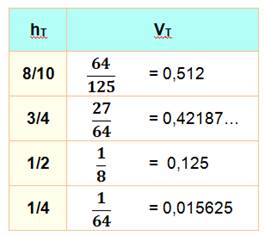
Un cornet de glace à partager entre toi et moi. Je déguste la première moitié du cône et te laisse la seconde. Est-ce bien équitable? J'en déguste combien en plus? En fait, le volume varie comme le cube de la hauteur. Calcul Résultats numériques	Cône hypothètique sans la boule qui dépasse et en supposant que le fond est bien rempli. Il faut laisser les 8/10 de la hauteur pour être équitable: moitié, moitié. En consommant la moitié supérieure de la hauteur, on absorbe les 7/8 de la glace contenue dans le cône. Il n'en reste qu'un huitième (0,125) pour son ami.

Cône maximum avec une surface donnée
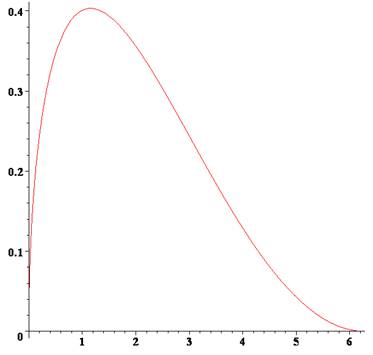
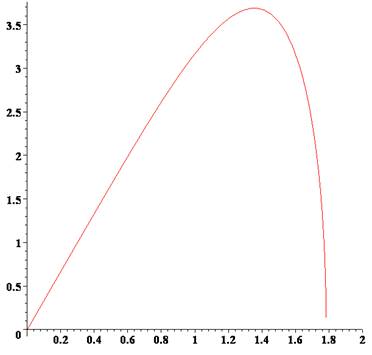
Question Avec une surface donnée (un morceau de tissu, par exemple), je souhaite former le cône de volume maximum. Que faire? Quelle hauteur? Quel rayon de base? Courbe La démonstration nécessite l'utilisation des dérivées à partir de l'expression de V = 1/3 R (S² – p ² R^4) Tracé de la courbe V = f(R) avec S = 10 Elle montre un maximum atteint pour 2 = 1,414…	Les calculs donnent h = 2 R

Patron du cône
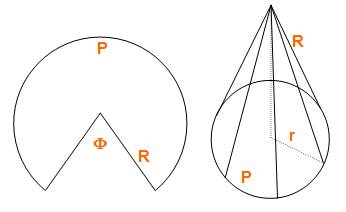
Patron Pour construire un cône, rien de plus simple: - Découpez un disque; - Évidez un secteur; Collez les deux segments.
Volume Question! Quel est le volume de ce cône? Périmètre du grand cercle Circonférence du secteur Périmètre de la base du cône	Pgc = 2 R P = 2 R - R (Angle exprimé en radians) P = 2 r
- Le bord du secteur sert de base au cône: les périmètres (P) sont égaux (comme le montre la figure) Ce qui permet de calculer le rayon de la base	P = 2 R - R = 2 r r = R - R / 2 = R (1 - / 2) = k . R avec k = 1 - / 2
- Passons à la hauteur, nécessaire pour calculer le volume	h² = R² - r² = = R² - k²R² = R² (1 – k²) h = R (1 – k²)
- Le volume Une formule bien compliquée Surtout lorsqu'on remplace k par sa valeur	V = 1/3 h . r² = 1/3 R (1 – k²) (k . R)² = 1/3 R^3 . k² . (1 – k²) = 1/3 R^3 . (1 - / 2))² . { 1 – (1 - / 2)² }
Exemple Pour R = 1 mètre, par exemple Courbe Courbe V = f ( ); calcul avec R = 1 Maximum atteint pour 66,1° (1,1536 radian) avec V = 0,403066…	= 90° = 1,57 radian V = 0,3896… m^3

Suite	Tronc de cône – Exemple de calcul Équations du cône Coniques
Voir	Cercle Cône, demi-sphère et cylindre Cylindre – double-cône = sphère Coniques Coniques – Théorème de Pascal Cône et triangle rectangle Cylindre Pyramides Vocabulaire de la géométrie
Sites	Cône de révolution (et plus) Cône – Homeomath Surfaces coniques Cone – from Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/GeomLAV/Objet3D/Cone1.htm