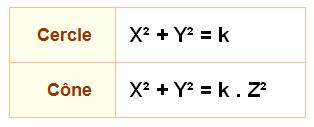|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Cône de révolution – Équations Le cône, en formules
mathématiques. Formules
|
|
|
||
|
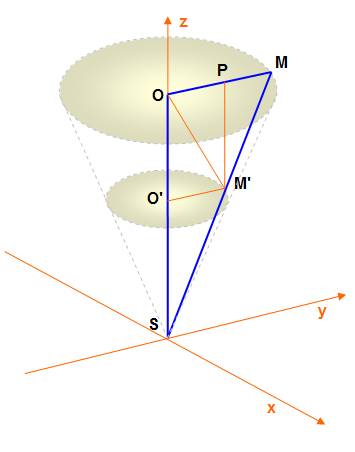
Équation X² + Y² – Z ² . tg² Calcul D OP² = X² + Y² D OM' / SO' = R / h OM' = OP OP / SO' = R / h SO' = Z OP / Z =
R / h OP = Z . R /h En
ég X²
+ Y² = Z² . R² / h² = Z² . tg² Axes cl X²
+ Y² = (h – Z)² . R² / h² |
Origine des axes au sommet du cône. R rayon du cercle de base. h hauteur du cône. a demi angle
au sommet.
|
|
|
|
||
|
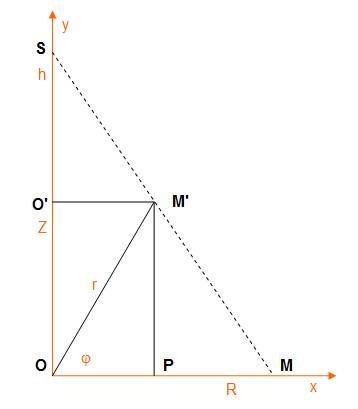
Équ r . cos C D cos r . cos Triangles
semblables SO'M' et SOM O'M' / OM = SO' /
SO OP / R = (h – Z) /
h En rempl r . cos = R – R/h . Z |
|
|
|
|
||
|
Équation r (cos Calcul Avec
le résult r
. cos
Exprimons
Z en fonction de phi Z = OO' = PM' = r
sin En rempl r . cos r . cos |
|
|
|
|
||
|
Équation X(t) = k . x(t) + (1- k) Y(t) = k . y(t) + (1- k) b Z(t) = k . z(t) + (1- k) c |
(a,b,c) sont les coordonnées du sommet. x(t), y(t), z(t)
= équation paramétrique de la directrice du cône (pas forcément un
cercle). X(t),Y(t),Z(t) = équation paramétrique d’un point du
cône. |
|
![]()
|
Retour |
|
|
Aussi |
|
|
Sites |
|
|
Cette
page |
![]()