|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
Partage du cercle en 12, 24, 48, 96 parts égales |
|
|
||
|
En six Segment
AB. Cercle
(A, AB); intersection C. Cercles
(C, AB) et (B, AB); intersections: D, E, F et G Avec ces
six points le cercle est partagé en six arcs égaux. Voir Partage en 3, 6, 12 NB. Le rayon
des cercles sera toujours égal à AB. Si vous dessinez avec un compas,
conservez son ouverture. |
|
|
|
En douze Perpendiculaire
en A à BC; intersections: H et I. Cercles
(H, AB) et (I, AB); intersections en J, K, L et M. Avec ces
six nouveaux points le cercle est partagé en douze arcs égaux. Disposant
des quatre cercles, on marque les intersections NOPQ qui sont les sommets du
carré circonscrit au cercle. |
|
|
|
|
||
|
Segment
NP et OQ (en vert). Quatre
intersections avec le cercle. Quatre
cercles de rayon AB et de centre ces quatre nouveaux points. Intersections
avec le cercle. Les 24
points sont présents. |
|
|
|
|
||
|
Corde
bleue Médiatrice
bleue; intersections avec le cercle. Reporter
le rayon du cercle sue la circonférence pour marquer les autres points |
|
|
|
|
||
|
Nouvelle
corde en bleu Médiatrice Nouvelle
intersection Les petits angles bleus mesurent 3,75° = 360° / 96. |
|
|
Cercle divisé
en 96 – Polygone régulier à 96 côtés
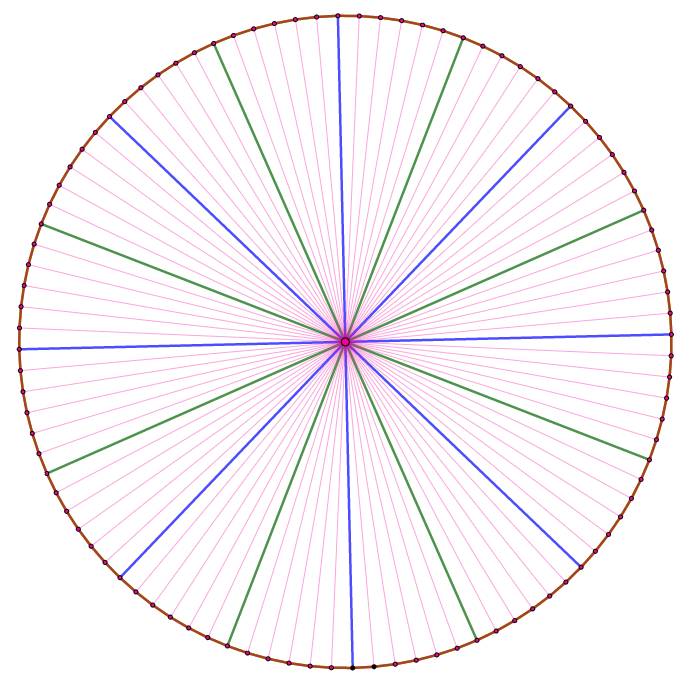
Voir Polygone
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()





