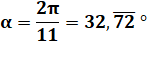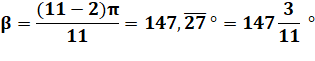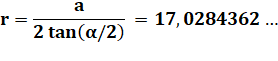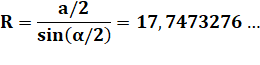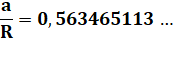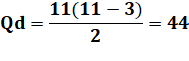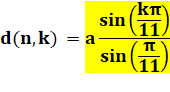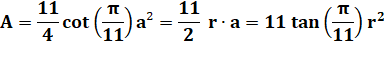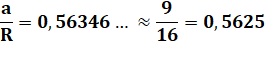|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
11-GONE Régulier / Hendécagone 11-gone ou hendécagone:
polygone à onze côtés ou onze angles. Du grec hendeka: onze; et gônia: angle, coin et proche de genou. Il est régulier si les côtés sont de même longueur et si les angles
ont même mesure.
|
Voir Nombre 11
|
Pi/11 =
16,3636…° |
2Pi/11 =
36,7272…° |
|
Formules diverses |
|
|
sinus |
0,2817325569 |
0,5406408175 |
|
|
|
cosinus |
0,9594929736 |
0,8412535328 |
||
|
tangente |
0,2936264930 |
0,6426609772 |
||
|
cotangente |
3,405687238 |
1,556030373 |
Voir Tables
trigonométriques / Relations entre
angles Pi/n
|
|
||
|
Longueur
côté: a = 10 (pour la figure) Angle au
centre
Angle
interne (somme 1 620 °)
Rayon du
cercle inscrit ou apothème
|
|
|
|
Diagonales Longueur
de la diagonale k, avec k la quantité de côtés interceptés par la diagonale. Quantité
|
|
|
||||||||||||
|
Aire 11 fois l'aire des triangles élémentaires |
|
= 9,36563990… a² |
||||||||||||
Voir Calcul de la longueur / Tables / Quantité
d'intersections des diagonales
Hendécagone avec ses quatre
variantes étoilées
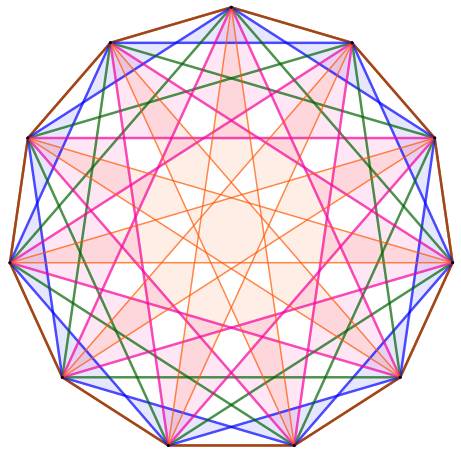
|
|
||
|
Le nombre 11 n'est pas un nombre de
Fermat, l'hendécagone régulier n'est pas constructible
à la règle et au compas. Le nombre 11 n'est pas un nombre de
Pierpont, l'hendécagone régulier n'est pas constructible par trisection. |
En revanche, l'hendécagone régulier est
constructible par neusis
et aussi par pliage origami. |
|
|
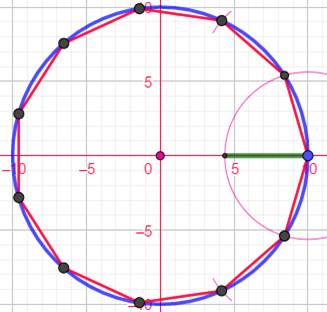
Pour une construction pratique et rapide, on peut
profiter du fait que la longueur du côté est voisine (un peu plus) de la
moitié du rayon du cercle circonscrit. On trace le cercle bleu puis le trait vert d'une
longueur un peu supérieure à la moitié du rayon. Pour un rayon de 10 m, on
prendra 5,63 m. Reporter cette distance sur la circonférence du
cercle avec un compas ou un bâton coupé à cette mesure. La construction de Dürer
est proche de celle-ci. |
|
|
|
||
|
Construction approchée très simple Cercle bleu. Rayon vert dont on prend:
Cette longueur est reportée sur la circonférence. Appréciation Dürer constate que:
Soit une erreur relative de 0,17% |
|
|
Voir Nombre
0,56 …
|
|
|||||||||||||||||||||||||||||
|
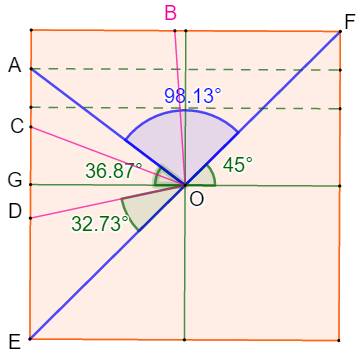
Construction approchée 1 (Figure) Basée sur l'approximation: Une approximation à 0,02 %, généralement
suffisante pour un tracé industriel. Procédé Un carré dont le haut est partagé en moitié, puis
encore en moitié pour donner le point A. L'angle AOF vaut 98,13° Bissectrice de AOF: point B Bissectrice de EOB: point C Bissectrice de EOC: point D L'angle EOD vaut 32,73° Reporter cet angle onze fois sur le cercle pour
obtenir l'hendécagone. Angle utilisé en degrés
|
Calcul des angles
|
||||||||||||||||||||||||||||
Constructions approchées par approximation du rapport a/R (méthode générale)
|
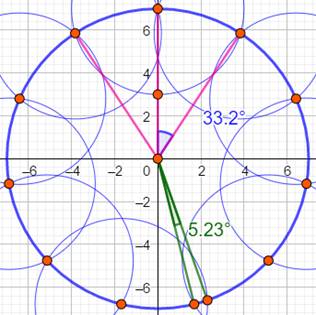
Construction approchée 2 (Figure) Basée sur l'approximation: Une approximation simple et peu précise Procédé Dessiner la
proportion 4/7 sur le rayon du cercle. Voir Construction
de la division d'un segment La construction est
approchée de 5,23° pour les deux derniers points. |
|
|
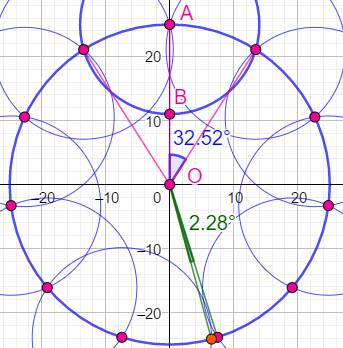
Construction approchée 3 (Figure) Basée sur l'approximation: Une approximation très certainement utilisée par
les architectes Gréco-romains. Procédé À partir du
point O, tracer un segment de 25 unités, point A et de 11 unités, point B. Cercle (O, OA) et cercle (A, AB). Les deux
intersections sont des sommets de l'hendécagone (approché). Report de cette
distance sur le cercle pour former les neuf autres points. La construction
est approchée de 2,28° pour les deux derniers points. |
|
|
|
||
|
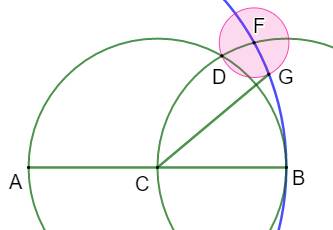
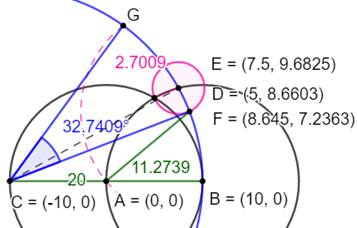
Construction approchée 4 Basée sur l'approximation: Construction la plus précise des quatre. Procédé (Figures en haut et au milieu) Cercle (A, AB)
en bleu qui recevra l'hendécagone. Cercle (C, CB) Cercle (B, CB) –
Intersections D et F Cercle (F, FD) –
intersection G La longueur CG
est la longueur du côté. Cette longueur
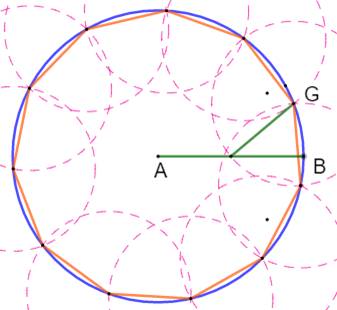
est reportée (figure du milieu) sur le cercle bleu. Calcul (Figure du bas) Les coordonnées
des points A, B et C sont indiquées. Cercle 1: (C,
CB) => (x+10)² + y² = 20² Voir Équation
du cercle Cercle 2: (A,
AB) => x + y² = 10² Cercle 3: (B,
AB) => (x–10)² + y² = 10² Point D,
intersection de C2 et C3: Point E,
intersection de C1 et C3: Distance DE Cercle 4: (E,
DE) => (x–xE)² + (y-yE)² = DE² Point F,
intersection de C1 et C4:
Distance AF Valeur théorique du côté de
l'hendécagone Appréciation des écarts Écart entre les deux derniers points sur la circonférence: 0,1495…° Longueur de l'arc: 0,0522 … pour une circonférence de 125,66… Soit 1 m sur une piste circulaire de 2,4 km. |
Détail de la construction (a = CG)
Construction de l'hendécagone
Mesures confirmant les calculs
|
|
Le relevé
de ces chiffres sur GeoGebra
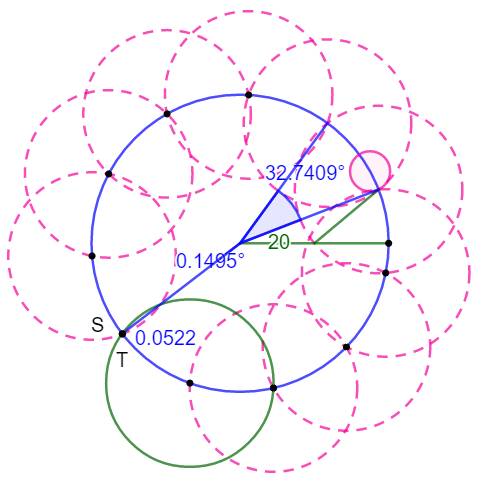
|
|
||
|
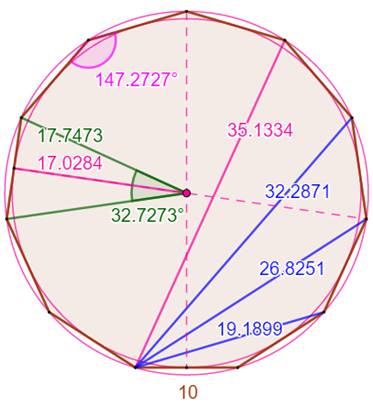
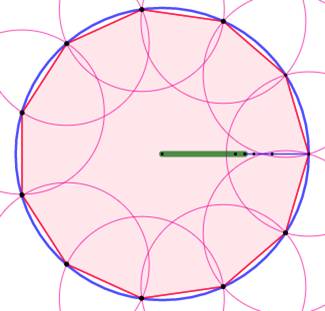
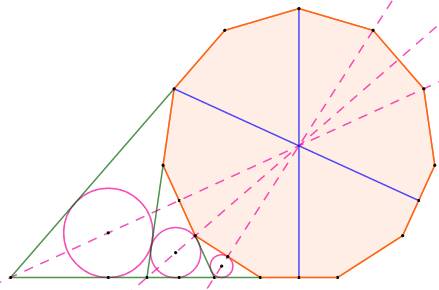
Sur ce
tracé, en prolongeant les côtés, on forme des triangles. Les
cercles inscrits sont dessinés en rose. Par
construction, leur centre est situé sur les bissectrices de leur angle. Les
bissectrices se dirigeant vers l'hendécagone et passent toutes par le centre
des cercles inscrit et circonscrit de l'hendécagone. Chacune
joint un sommet au milieu du côté opposé. |
|
|
Hendécagone sur la bordure du dollar canadien

![]()
|
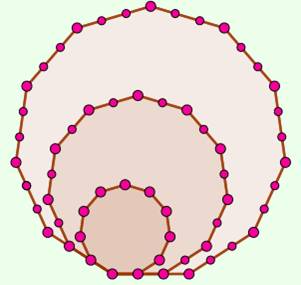
Nombres hendécagonaux Somme des points sur l'hendécagone et sur tous
les hendécagones adjacents internes.
Écart entre chaque nombre: 9n + 1 Les cinquante premiers 0, 1, 11, 30, 58, 95, 141, 196, 260, 333, 415, 506, 606, 715, 833, 960, 1096, 1241, 1395, 1558,
1730, 1911, 2101, 2300, 2508, 2725, 2951, 3186, 3430, 3683, 3945, 4216, 4496,
4785, 5083, 5390, 5706, 6031, 6365, 6708, 7060, 7421, 7791, 8170, 8558, 8955,
9361, 9776, 10200, 10633, 11075 Polynôme générateur
|
Voir Table des
nombres polygonaux / Polynômes
générateurs
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Document |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()