Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 15/01/2023 M'écrire Brèves de Maths

INDEX Cercle Géométrie	CERCLE – Propriétés
	Cercle	Fondements	Équations	Théorèmes
	Centre	Propriétés	Angles	Partage
	Vocabulaire	Sécante	Tangente	Corde et deux cercles
				Programme Scratch
	Cousines =>	Spirale	Hélice

Faites un double-clic pour un retour en haut de page

CORDE invariante & deux cercles sécants Deux cercles sont sécants. On découvre un triangle isocèle invariant. Sa base, une corde est de longueur constante. Cette corde est parallèle à une tangente particulière.
	Sommaire de cette page >>> Propriété >>> Corde parallèle à la tangente >>> Corde invariante	Débutants Géométrie Glossaire Géométrie

Propriété		haut
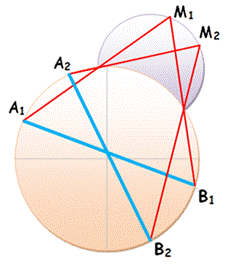
Deux cercles sécants. M est positionné n'importe où sur la circonférence d'un des cercles. On trace les sécantes MA et MB passant pas les deux intersections des cercles. Quelle que soit le point M, la corde AB a une longueur constante.

Voir Propriétés du cercle / Brève 48-958

Corde parallèle à la tangente		haut
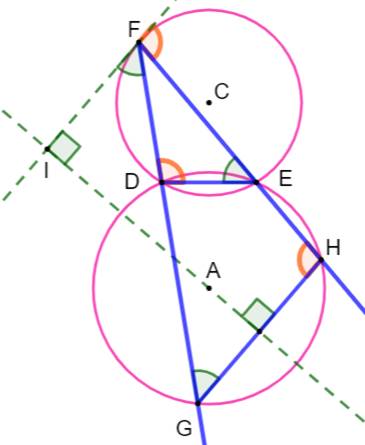
Deux sécantes qui engendrent deux triangles: FDE et FHG. Les trois angles verts sont égaux; de même que les trois angles oranges. Pourquoi ? Triangle inscrit FDE et tangente en F. Théorème de la corde-tangente: Angle IFD = angle FED (en vert) Quadrilatère cyclique DEHG Théorème des angles du quadrilatère cyclique: Angle FED = angle DGH (en vert) Tous les angles marqués en vert sont égaux. Les droites IF et GH font le même angle (vert) avec la sécante FG, elles sont parallèles.

Corde invariante		haut
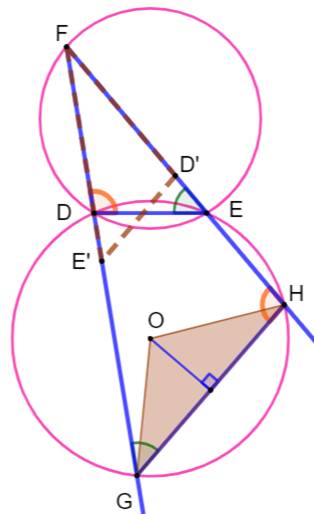
Les triangles FDE et FHG partagent des angles égaux deux à deux (verts, oranges et commun); ils sont semblables. Le triangle FDE retourné en FD'E', dessiné en pointillés, illustre cette propriété. Alors, les longueurs des côtés sont proportionnelles. En particulier pour les côtés DE et GH. Or, le segment DE est de longueur constante, en conséquence, il en va de même pour le segment GH. Le triangle GOH est un triangle isocèle de côté = R; sa base est invariante. Les trois côtes sont de longueur constante. Donc, le triangle GOH est invariant quelle que soit la position du point F. Avec le mouvement du point F, il subira une rotation autour de O tout en conservant la même forme et donc la même aire.

Haut de page (ou double-clic)

Retour	Cordes sécantes Deux cercles
Suite	Cercle – Équations Cercle – Fondements Cercles orthogonaux Inversion du cercle
Voir	Énigme des cercles qui tournent l'un sur l'autre Cercle – Index Géométrie – Index
Sites
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Cor2Cer.htm