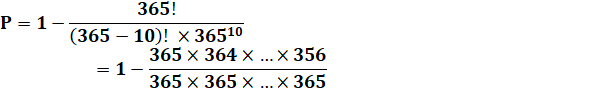|
||||||||||||||||||||||||||||||||
![]()
Aussi simple que cela, a priori
|
|
Voir
Pensées & humour
|
PRINCIPE DES TIROIRS ou principe des tiroirs
de Dirichlet-Schläfli ou principe des boîtes ou principe du trou de
pigeon
OUPS !
Je suis vraiment débutant Voir
un exemple simple et illustré du principe des
tiroirs Voir développements complets sur ce
principe des tiroirs |
Anglais:
The pigeon hole principle (PHP);
Allemand: Schubfachprinzip (das Schubfach: le
tiroir)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Exemples
Extension
Lecture: q
= plafond
du rapport m/n, ou l'entier supérieur
à ce rapport. Exemples
avec n = 3 tiroirs
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||
k est un
entier Exemples
|
|||||||||||
|
|
|
|
Ce principe est utilisé, en particulier,
pour démontrer le théorème
de Gelfond-Schneider sur les nombres transcendants. Utilisé pour prouver qu'un algorithme de
compression avec un certain taux de compression ne perd pas d'information. Une forme particulière est utile pour
résoudre les grilles de Sudoku. |
|
|
Énigme des croix dans le carré Parfois appelée énigme du parking |
|
|
Voici un exemple d'application du principe
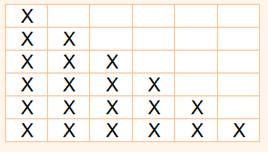
des tiroirs à une énigme classique. Énigme Un carré de N x N cases. On dessine
autant de croix que l'on veut dans ce carré. Affirmation: il existe au moins un cas où
deux lignes ou deux colonnes ou une ligne et une colonne possèdent la même
quantité de croix. Exemple
Sur cet exemple particulier, les lignes
sont différentes, les colonnes sont différentes. Très bien! Mais il existe
six couples de lignes et colonnes avec même quantité de croix. Solution Dans une ligne, on peut placer: 0, 1, 2, … N croix, soit N + 1 possibilités. Considérons que chaque possibilité est un tiroir. La première ligne compte une croix, elle rentre dans le tiroir 1. La deuxième ligne compte deux croix, elle rentre dans le tiroir 2. Etc. et même chose pour les colonnes. Bilan: je dois
ranger N lignes puis N colonnes dans N+1 tiroirs. Il y a bien plus de choses à ranger (2N)
que de tiroirs (N+1), alors, un des tiroirs contiendra au moins deux lignes
ou colonnes. |
|
Voir Carrés magiques
|
|
|
|
Un lemme évident: soit deux ensembles finis A
et B:
Un élément (un œuf) de plus et, il faut
forcément le mettre là où il y en a déjà un. Théorème Si n objets sont placés dans k boites,
alors il y a au moins une boite qui contient au moins q objets, avec :
q égal à la valeur plafond de n divisé par k. Exemple classique Dans tout groupe de 367 personnes, au moins
deux personnes sont né le même jour de l'année.
Théorème généralisé Plaçons au hasard n objets dans m boites.
La probabilité de placer un objet dans une boite est de 1/m. Alors, au moins
une boite contiendra plus d'un objet avec une probabilité:
Quelle est la probabilité d'avoir la même date
d'anniversaire parmi 10 personnes
On retrouve évidemment le passage à 50%
avec 23 personnes (valeur exacte: 22,7677 …). |
|
|
|
|
|
The pigeonhole principle states that if there are more pigeons than
there are roosts (pigeonholes), for at least one pigeonhole, more than two
pigeons must be in it. This is a fundamental tool of elementary discrete
mathematics. It is also known as the Dirichlet Drawer Principle. Pigeonhole Principle If k + 1 or more objects are placed into k boxes, then there is at
least one box containing two or more objects. |
|
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()