|
|||||||||||||||||||||||||||||||||||||
![]()
|
SUDOKU
- DOUBLETS Dans
un premier temps, une grille de Sudoku se résout en
cherchant les possibilités évidentes pour placer un chiffre. Puis, on en passe
par l'inscription des chiffres possibles dans les cases. C'est
à ce stade qu'intervient le principe des
tiroirs; principe aménagé au cas du Sudoku. Comment
éliminer des chiffres
sur la base d'observations de doublets ou de triplets de chiffres? La
rencontre de doublets est extrêmement fréquente et l'identification des
doublets est indispensable pour résoudre les grilles de Sudoku. |
|
|
|
|
|
|
Avec ce résumé vous savez tout. Continuez la lecture pour
approfondir le sujet.
|
|
|||||||||||||||||||
|
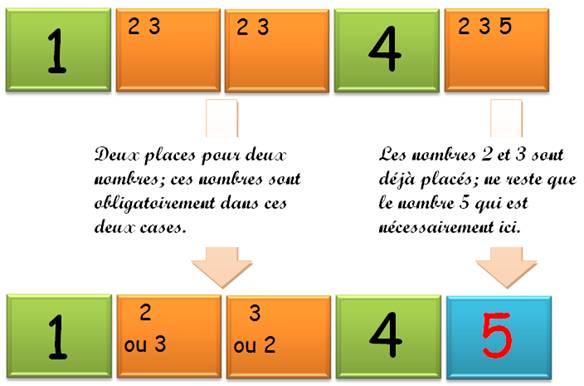
Rappel PRINCIPE DES TIROIRS |
Si j'ai
trois balles à placer dans deux tiroirs
Quelle que
soit la manière de s'y prendre. On observe qu'il y a toujours au moins deux
balles dans un tiroir (2 ou 3). Ce qui est logique
car au mieux je mets une balle dans chaque tiroir et quand vient le moment de
placer la troisième, elle ira dans l'un des tiroirs. Or, il y a déjà une
balle, ce qui fera deux balles dans l'un des tiroirs. |
Trois
balles dans deux tiroirs. Voici
les quatre cas possibles:
Vous constatez
qu'il y a toujours au
moins deux balles dans un des tiroirs (en rouge), l'un ou l'autre. |
|||||||||||||||||
|
SUDOKU |
Deux
règles s'ajoutent au Sudoku:
Voici une
illustr |
||||||||||||||||||
|
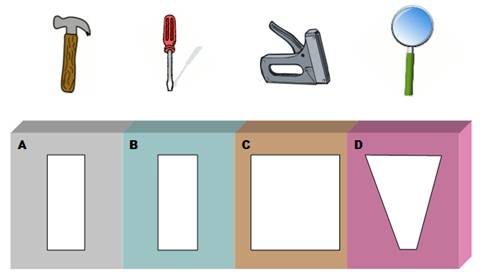
Illustration |
Ranger les outils à raison de un par compartiment. Résolution:
Évident!
Oui, eh bien transposons au Sudoku. Mettre
les chiffres 1, 2, 3 et 4 dans les cases, un par case et selon les
possibilités de rangement indiquées pour chaque case.
Les
chiffres 1 et 2 peuvent Mais
si je place l'un d'eux en première case, l'autre est automatiquement et
obligatoirement en deuxième case. Alors, aucun autre chiffre ne peut aller
dans ces deux premières cases. Les
chiffres 1 et 2 sont donc forcément dans ces deux premières cases et nulle
part ailleurs. Vous
pouvez effacer les chiffres 1 et 2 dans les autres cases.
|
||||||||||||||||||
|
DOUBLET |
Le constat exposé ci-dessus permet de résoudre certains cas au Sudoku. Un doublet permet d'éliminer la
présence de ses propres chiffres sur le reste de la ligne, de la colonne ou
de la région. Le
1 et le 2 (doublet) est bien dans les deux premières cases et nulle part
ailleurs. |
D
Le
doublet (1,2) est présent dans les
deux premières cases, alors ces deux chiffres sont là et pas ailleurs
|
|||||||||||||||||
Voyons tout cela en détails
|
|
||||||||||||||||||
|
CASES PARFAITES (Deux chiffres d |
CHIFFRES CONCENTRÉS (Aucun des deux chiffres |
|||||||||||||||||
|
Un doublet
est formé de deux chiffres dans deux cases, sans autres chiffres dans les
mêmes cases. Formées ainsi, les cases sont parfaites
. Lorsque
les chiffres du doublet ne sont présents que dans deux cases, ils sont dits concentrés: => Dans
ce cas les deux chiffres sont là et pas ailleurs (de manière évidente). |
Chiffres du
doublet repérés en rouge
Conclusion
évidente
Les
chiffres 1 et 2 sont d Explic
|
|||||||||||||||||
|
CASES PARFAITES (Deux chiffres d |
CHIFFRES DILUÉS (Les deux chiffres sont aussi ailleurs) |
||||||||||||||||
|
Lorsque
les chiffres du doublet sont aussi présents dans d'autres cases, ils sont dilués: => Dans
ce cas les deux chiffres sont là malgré tout et pas ailleurs. En effet, en essayant 1 en première case, le 2 vient en
deuxième case éliminant la possibilité d'un 1 ou d'un 2 plus loin sur la
ligne. Même chose avec deux. Dans les deux cas les 1 et 2 ne sont pas ailleurs. |
Chiffres du
doublet repérés en rouge
Conclusion
Explic
|
|
CASES ALTÉRÉES (les deux chiffres ne sont p |
CHIFFRES CONCENTRÉS (Aucun des deux chiffres ailleurs) |
||||||||||||||||
|
Lorsque
les cases du doublet contiennent d'autres chiffres, les cases sont altérées: => Si les
chiffres du doublet sont concentrés, alors
dans ce cas les deux chiffres sont là malgré tout et pas ailleurs. Le 1 ne peut être que d |
Chiffres du
doublet repérés en rouge
Conclusion
Explic
|
|
CASES ALTÉRÉES (les deux chiffres ne sont p |
CHIFFRES DILUÉS (Les deux chiffres sont aussi ailleurs) |
||||||||||||||||||||
|
Si les
cases sont altérées et les chiffres dilués: =>
Alors, pas de conclusion possible. D' |
Chiffres du
doublet repérés en rouge
Conclusion
Explic
P |
|
|
|||||||||||||
|
Revoyons en un coup d'il les trois cas de conclusion
possibles. Les chiffres 1 et 2 du doublet sont bien dans les deux
premières cases et pas ailleurs. |
P
P
Altéré concentré
|
||||||||||||
|
Voyons tous les cas en un schéma. Dans tous les cas, il est possible de conclure que les chiffres
du doublet sont dans leurs cases, sauf dans le cas altéré dilué. En pratique, on peut conclure et isoler
les deux chiffres du doublet dans deux cases. Lorsque - Le doublet est pur. - Les chiffres du
doublet bavent dans les autres cases. - Le doublet est h M |
OUI, les chiffres sont
dans les cases du doublet Si le doublet est
parfait (pas d'autres
chiffres dans ses cases), même si ses chiffres se retrouvent aussi ailleurs. Ou Si les chiffres sont concentrés
dans leurs cases, même si elles sont aussi occupées par d'autres chiffres. |
||||||||||||
Bilan
|
Le cas du doublet est assez simple, n'est-ce pas? Le cas du triplet
n'est pas plus compliqué. Sauf que le triplet peut se présenter sous forme
complète ou tronquée. |
![]()
|
Suite |
|
|
Voir |
SUDOKU |
|
Aussi |
|
|
Cette page |
![]()