NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/05/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Dénombrement
Débutants Général	Principe des TIROIRS			Glossaire Général
INDEX Dénombrement	Débutant	Exemples	Connaissances	Nb en 00 ..01
	Introduction	Divisibilité 10	Divisibilité 2n	Divisibilité n
	Points	Nombres de Ramsey
		Sommaire de cette page >>> Dans sa plus simple expression >>> Formulation à un objet >>> Approche à deux >>> Les trois enfants >>> Tiroirs avec des billes >>> Formulation à deux objets

Principe des tiroirs

Page spéciale pour DÉBUTANTS

Je ne suis pas novice => Développement en dénombrement

Le principe en bref			haut
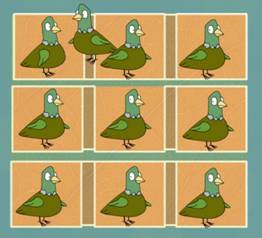
Principe des tiroirs. Se dit pigeonhole principle (principe du pigeonnier) en anglais Dans la situation de gauche, où se place le dixième pigeon ? Nécessairement dans l'un des neuf trous ! Un des trous contiendra au moins deux pigeons.		Dans la situation de droite, le même principe s'applique même pour plus de pigeons. Si n est la quantité de trous: à gauche: n + 1 pigeons. à droite: 2n + 1 pigeons.

Voir Brève 50-990

DANS SA PLUS SIMPLE EXPRESSION

1 tiroir, 2 jouets

Il semble évident que

Dans 1 tiroir, si j’ai deux jouets à ranger, ils seront tous les deux dans ce tiroir ! Eh oui!

2 tiroirs, 3 jouets

Pas besoin de beaucoup de théorie pour affirmer que:

Même en répartissant bien les jouets dans les tiroirs, il y a un qui contiendra au moins deux jouets, de toute manière.

J’ai trois jouets à ranger dans deux tiroirs.

Je peux en mettre un dans chacun des tiroirs.

Et, le troisième ira forcément dans un tiroir déjà occupé.

Dis autrement, un des tiroirs contiendra au moins deux objets; il pourrait même en contenir trois.

3 tiroirs, 4 jouets

Pouvez-vous sauter le pas et conclure pour trois tiroirs?

Même en répartissant bien les jouets dans les tiroirs, il y a un qui contiendra au moins deux jouets, de toute manière.

Je commence à mettre un jouet dans chacun des tiroirs et le quatrième ira forcément dans un tiroir déjà occupé.

Formulation – UN OBJET

Si je dispose d'un objet de PLUS que de tiroirs,

il y aura au moins un tiroir contenant deux objets.

APPROCHE à DEUX
Isabelle et Clément discutent. Dans la pièce : 1 fille et 1 garçon.
Arrive un troisième enfant: Une fille OU un garçon ! Évidemment deux possibilités.		? ou ?
ou	C’est une FILLE Total deux filles.	2 filles et 1 garçon
	C’et un GARÇON Total deux garçons.	1 fille et 2 garçons
Dans les deux cas, il y a deux personnes du même sexe.		Dans un cas comme dans l’autre, il y deux personnes du même sexe

LES TROIS ENFANTS

Si trois enfants se trouvent ensemble.

Il y a 4 possibilités, mais …

Il a au moins
deux filles ou
deux garçons.

Cas 1				3 filles
Cas 2				2 filles et 1 garçon
Cas 3				1 fille et 2 garçons
Cas 4				3 garçons

Formulation

Parmi trois personnes, il y en a toujours deux du même sexe.

Ou, autre formulation

Pour avoir deux personnes du même sexe, au moins, dans un groupe, il suffit de trois personnes.

Attention!

Il y a bien deux personnes du même sexe, par contre, il y a une chose que je ne sais pas dire : c’est de quel sexe il s’agit !

Combien faudrait-il faire entrer de personnes dans la pièce pour avoir deux filles ? Réponse : une infinité, si ce ne sont que des garçons qui entrent et jamais de filles …

TIROIRS – Avec des Billes
J’ai des billes rouges et des billes vertes dans un sac. Combien de billes faut-il prendre pour être sûr d’en avoir deux de la même couleur ? Je suis perdu !!! Avec, l’exemple de garçons et des filles, c’était évident. J’ai bien compris. Mais là avec les billes de deux couleurs c’est un peu plus dur. Avec les billes, pas si clair, et pourtant … Pensez à mettre un petit dessin de fille sur les billes rouges et un dessin de garçon sur les billes vertes, et, avec les billes de deux couleurs, vous êtes exactement dans le même cas que filles et garçons. Parmi des trois billes de deux couleurs, il y en a forcément deux de la même couleur.

Formulation – Deux objets

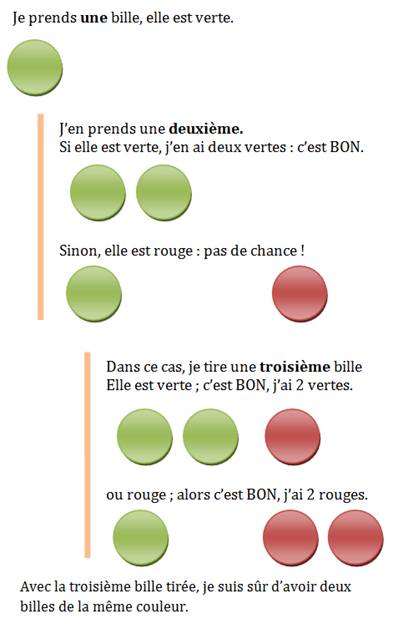
Cas de l’exemple des billes

Avec des billes de deux couleurs, il suffit d’en tirer trois pour être certain d’en avoir deux de la même couleur.

Généralisation

Avec des objets de DEUX types, il suffit d’en prendre trois pour être certain d’en avoir deux du même type.

Exemples (et précautions)

Avec trois pions sur un damier, deux sont sur la même couleur (noir ou blanc). Je tire à pile ou face. Au bout du troisième essai, deux, au moins, seront de même nature: ou pile ou face. Choix entre le cours de maths ou celui d'anglais. Avec trois élèves seulement, il y aura deux élèves au moins dans l'un des cours. Bière ou coca? Avec trois consommateurs, deux (ou trois) boirons l'une des deux boissons. Parmi trois poussins, deux au moins deviendront soit poulets (coq), soit poulettes (poules). Les couteaux et les fourchettes sont mélangés dans le même tiroir, il me suffit de prendre trois ustensiles pour être sûr d’en avoir deux du même type. Mais, attention, si je tiens à avoir des couteaux, il me faudra peut-être vider le tiroir… Trois parachutistes sautent au-dessus d’un lac, deux au moins sont soit dans l’eau soit sur la terre ferme. Trois lampes dans le salon. J’arrive et bascule les interrupteurs. Deux lampes au moins seront ou allumées ou éteintes. Parmi trois bits en numération binaire, deux sont du même type, soit 0 soit 1.

Voir Théorie des nombres / Exemples

Voir	Dénombrement et tiroirs Sudoku et tiroirs Exemples d'applications
Aussi	Compter Jeux – Index
Cette page	http://villemin.gerard.free.fr/aMaths/Denombre/Tiroir/Debutant.htm