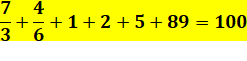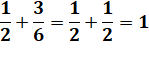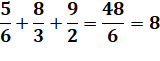|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Fractions avec les chiffres de 1 à 9 Leurs sommes Comment atteindre 100 par additions? Amusement avec les chiffres et les fractions. Peut être utile pour certains jeux de
nombres. Comme, par exemple: faire 100
avec additions avec les neuf chiffres.
|
|
|
||
|
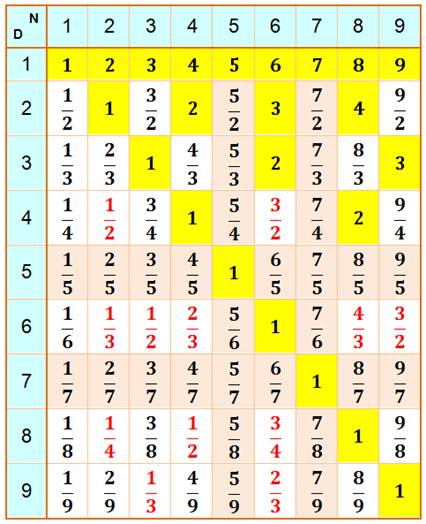
Ce
tableau à double entrées indique toutes les fractions formées avec
Sur les
81 valeurs dans le tableau, il y a:
Les
nombres premiers comme 5 et
7 (lignes et colonnes ocre) ne produisent que des fractions irréductibles. |
|
|
|
|
||
|
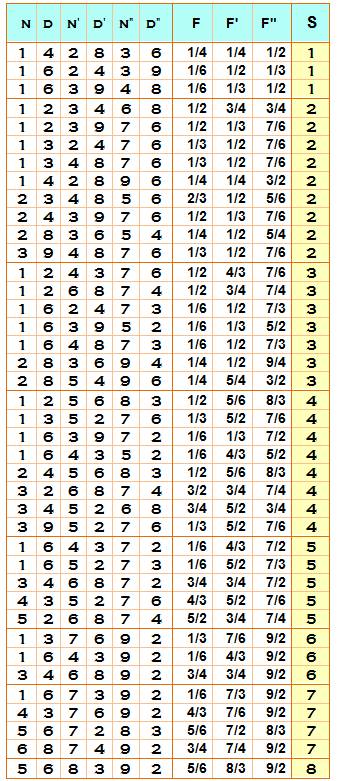
Ce
tableau indique toutes les sommes de deux fractions, réduites ou non, faites
de quatre chiffres tous différents. Exemple:
Propriétés Sur 3
645 sommes de ces fractions, seules 37
sont retenues comme ayant des chiffres différents et produisant une somme
entière. Le nombre
entier le plus grand est 6 avec 6/4 + 9/2. Notez l'esprit de ce tableau: on a
aussi, 6 = 3/2 + 9/2, mais avec cette configuration,
le chiffre 2 est présent deux fois ce qui est contraire à notre exigence. En rouge,
les fractions irréductibles. Aucune somme n'est constituée de deux fractions
irréductibles. |
|
|
|
|
||
|
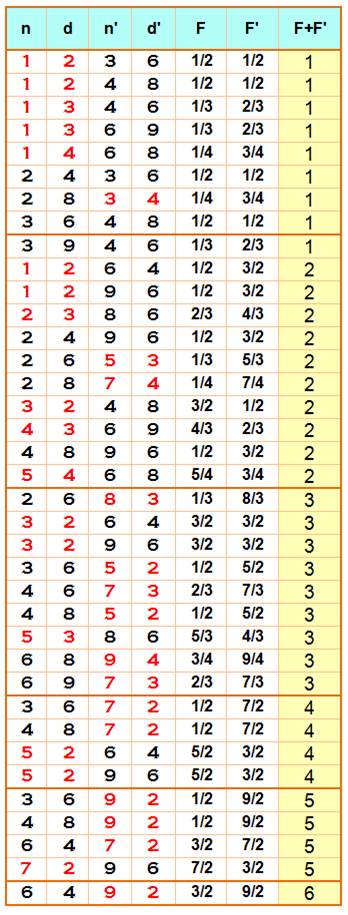
Ce
tableau indique toutes les sommes de trois fractions, réduites ou non, faites
de six chiffres tous différents. Exemple (la dernière):
Voir Réduction au
même dénominateur Propriétés Sur 84
480 sommes de ces fractions (non redondantes), seules 40 sont retenues comme
ayant des chiffres différents et produisant une somme entière. Le nombre
entier le plus grand obtenu de la sorte est 8. |
|
|
Voir Fractions
pannumériques minimales
![]()
La suite est du niveau collège
Applications
|
Comment
atteindre la valeur 100 avec
les neuf chiffres, mais avec la
seule addition? Faisable qu'en
introduisant les fractions.
Voyons
cela. |
|
|
||
|
Dans un
premier temps, on examine la possibilité d'atteindre la somme 100 avec les
neuf chiffres. Leur simple somme: Pour atteindre 100, il faut trouver autre chose.
On utilise la concaténation des chiffres,
comme 1 et 2 qui peuvent se concaténer en 12 ou 21. Remarquons que seules les
concaténations à deux chiffres sont possibles sans dépasser la valeur 100. On va montrer que, même avec la concaténation,
c'est impossible. Aucune configuration du type: En effet, ils sont neuf chiffres avec cinq impairs, c'est pourquoi la
somme (45) est impaire. Pour atteindre 100, nombre pair, il faut opérer une
concaténation produisant un nombre pair tout en supprimant un nombre impair.
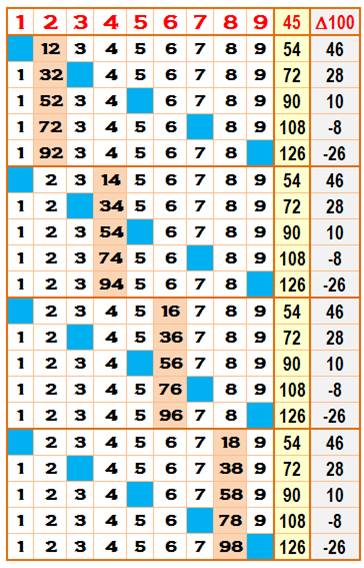
Ce sont les possibilités illustrées dans le tableau ci-contre. Observez que,
pour chaque nombre pair, il y a cinq possibilités chacune donnant
répétitivement la même somme. La somme 100 n'est jamais atteinte avec une seule
concaténation. Une deuxième est nécessaire. Elle doit conserver la parité de
la somme. Elle ne peut s'effectuer qu'entre deux nombres pairs restants. Tous
les essais sont vains. Pour information Dans toutes les solutions à huit chiffres, c'est
le chiffre 8 qui est absent. |
Sommes à une concaténation
Les sept solutions à huit chiffres
|
|
|
|
||||||||||||||||||||
|
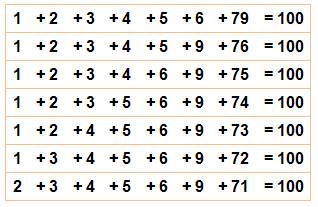
Faire 100
avec les neuf chiffres et uniquement des additions devient faisable en
introduisant des fractions. Ce
tableau donne quelques exemples. La
colonne blanche isole les fractions utilisées avec la somme partielle
obtenue. Notez toutes les variantes possibles en intervertissant les unités.
Voir exemples en ligne 2 et en ligne 4. |
|
|||||||||||||||||||
Exemples de
somme de deux fractions entières avec chiffres différents
|
La
plus grande avec numérateur à deux chiffres:
Les
suivantes:
Parmi
les plus petites (la somme et les deux fractions couvrent huit chiffres sur
dix):
Il
existe 115 telles sommes de fractions. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()