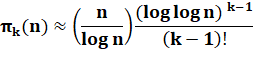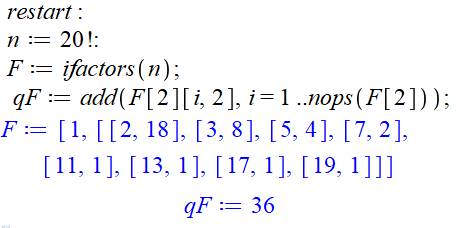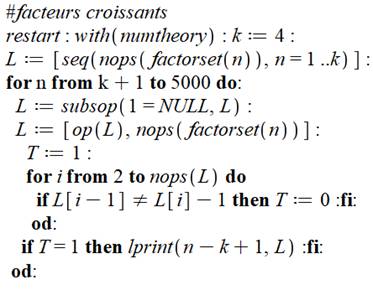NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/03/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Premiers	Nombres PRESQUE PREMIERS Quantité de facteurs premiers			Glossaire Premiers
INDEX Premiers Nombres Types de nombres premiers		k–presque premiers	Facteurs	Probablement P.
		Sommaire de cette page >>> Nombres presque premiers >>> Liste des nombres k-premiers >>> Nombre de 2 à 100 avec quantité de facteurs >>> Nombres premiers avec facteurs répétés en progression >>> Nombres composés avec facteurs uniques en progression >>> Écart entre nombres de même quantité de facteurs >>> Programme de recherche de la quantité des facteurs >>> Programme de recherche des k-uplets de facteurs croissants

Famille	Nombre / Diviseurs / Multiplicatif / Premiers … / Types de nombres premiers et cousins
Définition	NOMBRES PRESQUE PREMIERS Nombre qui est soit premier, soit semi premier Un nombre semi premier est le produit de deux nombres premiers. Non nécessairement distincts. NOMBRES k–PRESQUE PREMIERS Généralisation aux nombres comportant k facteurs, répétés ou non.
Propriétés	Les puissances k de 2 sont les plus petits k-presque premiers. Il existe une infinité d'entiers n tels que n² + 1 soit un nombre presque premier (théorème d'Iwaniec et Richert). Théorème de Hardy – Ramanujan (1917) Une bonne approximation de la quantité de facteurs distincts d'un nombre n est en log (log n). La quantité de nombres k-presque premiers Pik(n) est asymptotiquement égal à (selon Landau):
Exemples	6 = 2 x 3 2–P 8 = 2 x 2 x 2 3–P 24 = 2 x 2 x 2 x 3 4–P

Anglais	k – Almost Prime
Voir	Place de ces nombres parmi les autres premiers Types de nombres selon leurs facteurs Nombres semi-premiers et k-presque-premiers développement Les k-presque-premiers et les pseudo-premiers

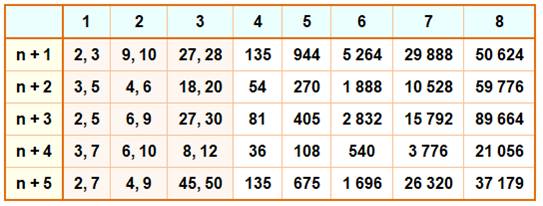
Liste 50 premiers k-presque premiers pour k de 1 à 5
Les nombres 1 – p sont les nombres premiers. Les nombres 2 – p ont deux facteurs, répétés ou non.

Nombres de 2 à 100 avec quantité de facteurs (OMÉGA) et quantité de facteurs uniques (Oméga)

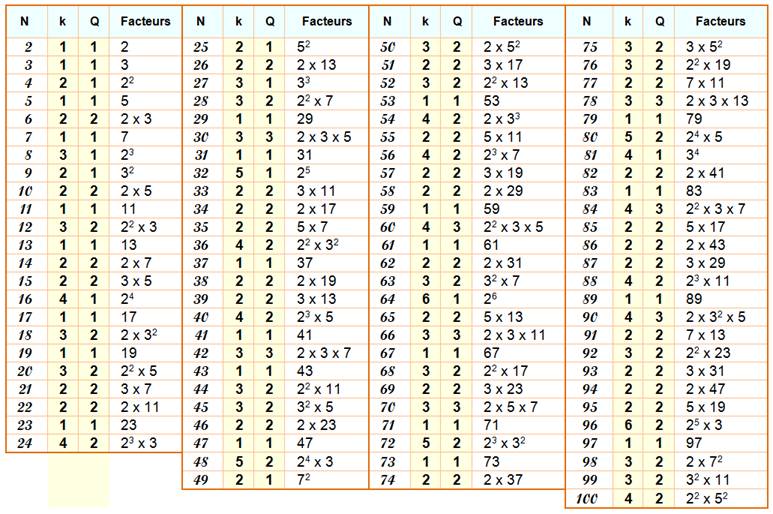
Fonctions arithmétiques notées: oméga de n: pour la quantité de facteurs uniques (factorset), et oméga majuscule de n: pour la quantité de facteurs répétés. Tableau (ici k = oméga majuscule et Q = oméga minuscule) Records de quantité de facteurs uniques (primorielles): [2, 1], [6, 2], [30, 3], [210, 4], [2 310, 5], [30 030, 6], [510 510, 7],… Records de quantité de facteurs répétés (puissances de 2): [2, 1], [4, 2], [8, 3], [16, 4], [32, 5], [64, 6], [128, 7],… Coefficient de puissance des facteurs: k^Q = [1, 1], [2, 1], [3, 1], [4, 2], [5, 1], [6, 4], [7, 1], [8, 3], [9, 2], [10, 4], [11, 1], [12, 9], [13, 1], [14, 4], [15, 4], [16, 4], [17, 1], [18, 9], [19, 1], [20, 9], [21, 4], [22, 4], [23, 1], [24, 16], [25, 2], [26, 4], [27, 3], [28, 9], [29, 1], [30, 27], [31, 1], [32, 5], [33, 4], [34, 4], [35, 4], [36, 16], [37, 1], [38, 4], [39, 4], [40, 16], [41, 1], [42, 27], [43, 1], [44, 9], [45, 9], [46, 4], [47, 1], [48, 25], [49, 2], [50, 9], [51, 4], [52, 9], [53, 1], [54, 16], [55, 4], [56, 16], [57, 4], [58, 4], [59, 1], [60, 64] … Par exemple pour 60 = 2^2 x 3 x 5 => k = 4 et Q = 3 => 4^3 = 64. Valeur qui est supérieure à n = 60. Liste des nombres n < k^Q : 60, 120,210, 420, 840, 1260,1680, 2310, 2730, 3360 … Même quantité de facteurs répétés [20, 21, 22] ... [33, 34,35, 36] … [54 à 58] … [91 à 96]: même quantité de facteurs répétés (2).

Voir Programmes de recherche ci-dessous

Nombres premiers suivis de nombres avec quantité de facteurs répétés en progression

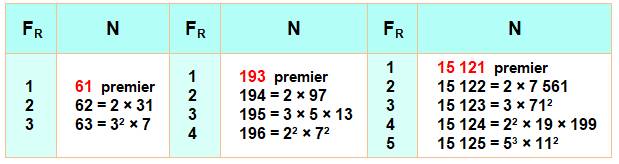
Tête de liste

Les trois plus petits nombres avec facteurs répétés (F_R) jusqu'à 3, 4 et 5.

Suivant: 838 561

Premiers et (1, 2, 3)

[61, 73, 193, 277, 397, 421, 613, 661, 757, 1093, 1237, 1453, 1657, 2137, 2341, 2593, 2797, 2917, 3217, 4177, 4621, 5233, 6121, 6133, 6217, 7057, 7537, 8101, 8317, 8353, 8521, 8677, 8893, 9013, 9277, 9721, 9817,…]

Premiers et (1, 2, 3, 4)

[193, 421, 661, 1093, 1657, 2137, 2341, 2593, 6217, 7057, 8101, 9817, 12421, 12853, 15121, 16033, 16417, 17257, 17881, 19813, 20641, 21817, 25033, 25657, 27337, 28921, 30661, 31081, 31321, 31333, 32377, 35521, 36457, 38281, 40693, 45553, 46261, 47017, 47161, 47713, 48121, 50821, 51481, 52321, 54421, 55633, 56857, 59833, 60217, 61681, 66361, 75721, 79801, 80713, 82021, 85333, 91081, 91381, 91513, 97777, 97813,…]

Premiers et (1, 2, 3, 4, 5)

[15121, 35521, 52321, 117841, 235441, 313561, 398821, 516421, 520021, 531121, 570601, 623641, 761113, 838561, 941041,…]

Nombres composés suivis de nombres avec quantité de facteurs uniques en progression

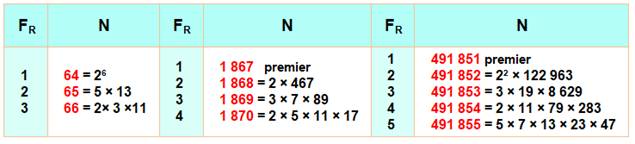
Tête de liste

Les trois plus petits nombres avec facteurs unique (F_R) jusqu'à 3, 4 et 5.

Suivant: 17 681 491

Nombres en (1, 2, 3)

[64, 103, 128, 163, 193, 271, 283, 313, 343, 383, 397, 463, 523, 607, 613, 625, 661, 691, 733, 757, 823, 967, 1024, 1093, …]

Nombres en (1, 2, 3, 4)

[1867, 1999, 3217, 4057, 4177, 5107, 5233, 5527, 6367, 7537, 8167, 8677, 8863, 9391, 9643, 9721, 9787, 10567, 11047, 11701]

Nombres en (1, 2, 3, 4, 5)

[491851, 521881, 1667641, 1898761, 2173531, 2203351, 2538511, 2562661, 2686603, 2914831, 3154147, 3280231, 3351631, 3505771, 3598591, 3746167, 3843451, 3904897, 3917833, 3945301, 3963241, 4057357, 4275547, 4295911, 4325317, 4475467, 4558291, 4726081, 4735441, 4751743, 4794247, 4896811, 4939567, 5118577, 5188543, 5304841, 5331511, 5430421, 5437351, 5810647, 5964241, 6137491, 6504571, 6559081, 6786721, 6818731, 6878491, 6886771, 6954391, 7032931, 7038181, 7109917, 7120417, 7129651, 7179091, 7248601, 7335961, 7339867, 7342177, 7478467, 7576081, 7660231, 7674481, 7955581, 7981411, 8110441, 8322661, 8349337, 8484577, 8489191, 8595451, 8627251, 8631151, 8632411, 8681131, 8837011, 8952511, 8995411, 9074347, 9133771, 9201601, 9238771, 9245947, 9283831, 9430627, 9680491, 9927991, 9953401, …]

Écart entre nombres de même quantité de facteurs

On cherche le premier couple de nombres (n et n + k) qui ont la même quantité de facteurs premiers multiples.

Exemple: 270 et 272 (k = 2): 270 = 2.3³.5 => 5 facteurs et 272 = 2⁴.17 => 5 facteurs; ce couple est le plus petit ayant cinq facteurs premiers en les comptant tous.

Pour n + 2, après 59 776 on a: 101 248, 406 782, 6 581 248, …

Exemple: 101 248 = 2^.7.7.113 et 101 250 = 2.3⁴.5⁴ , chacun ayant 9 facteurs.

DicoNombre: 135, 270, 944, 1 888

Nombres consécutifs avec même quantité de facteurs (non répétés)

On cherche 3 nombres consécutifs (triplet) ayant la même quantité de facteurs sans répétition.

Deux facteurs

Trois facteurs Quatre facteurs

Programme de recherche de la quantité des facteurs et de leur coefficient de puissance (Maple)
	Commentaires Appel des logiciels de théorie des nombres. Déclaration de la liste L qui recevra . Boucle d'analyse de n de 1 à 10, par exemple. N reçoit les facteurs du nombre n en cours d'analyse (la liste en partie 2). Quantité en q. En f, on additionne tous les exposants des facteurs (ils sont en deuxième position). Calcul de la puissance. Mise en liste du couple A associé à n. Impression de la liste. En bleu le résultat du traitement.
		Ce programme produit la factorisation d'un nombre et calcule la quantité de facteurs premiers multiples. Ainsi factorielle (20) comporte 36 facteurs répétés.

Voir Programmation – Index

Programme de recherche des k-uplets de facteurs uniques croissants
	Commentaires Redémarrage, appel aux logiciels de théorie des nombres. Ici le k-uplet est un quadruplet (k = 4). La liste L est remplie des k premières quantités (nops) de facteurs uniques (factorset). La séquence construit toutes les valeurs de 1 à k. Lancement de la boucle d'analyse n à partir de k+ 1 (les k premiers sont déjà dans L en tant qu'initialisation). Pour maintenir k valeur dans la liste, on retire le premier (subsop) et on introduit le suivant. Un témoin est mis à 1, faisant l'hypothèse que les quantités de facteurs vont croissant. Analyse des k valeurs de L et test si chacun est égal au précédent plus 1. Sinon, le témoin T est mis à zéro. Si T s'est maintenu à 1, les k nombres de L sont croissants et on imprime la valeur n de début de liste. En bleu, le résultat du traitement.

Programmes plus rapides (Maple 16)
restart; with(NumberTheory): kt := 0: L := []: for n to 1000 do q := NumberOfPrimeFactors(n); if q = kt+1 then kt := kt+1 else kt := 0 end if; if kt = 3 then L := [op(L), n-kt+1] end if end do: print(L): [61, 73, 193, 277, 397, 421, 613, 661, 757]	restart: with(NumberTheory): L := []; for n to 500 do q := seq(nops(PrimeFactors(n+i)), i = 0 .. 2); if [q] = [1, 2, 3] then L := [op(L), n] end if end do: print(L): [64, 103, 128, 163, 193, 271, 283, 313, 343, 383, 397, 463]

Suite	Nombres probablement premiers
Voir	Nombres premiers Semi premiers Nombres multi-premiers
Site	Almost prime – Wikipedia – Avec liste des k-almost primes et leurs pages sur l'encyclopédie OEIS OEIS A001358 - Semiprimes (or biprimes): products of two primes. OEIS A177871 – Numbers n such that bigomega(n)^omega(n) > n Almost Prime – Wolfram MathWorld Asymptotic density of k-almost primes – mathoverflow
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremPreq.htm