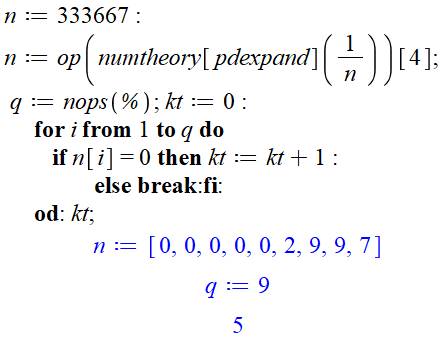NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/01/2024 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Types de Nombres
Débutants Premiers	NOMBRES PREMIERS				Glossaire Premiers
INDEX Premiers Nombres	Premier	Sophie Germain	Premier sûr	Premiers de Chen
		Luhn	Unique
		Sommaire de cette page >>> Nombres premiers uniques >>> Liste >>> Programmation

Nombres premiers uniques

Famille

Nombre / Diviseurs / Multiplicatif / Premiers

Approche

Nous analysons une propriété de l'inverse (1/p) des nombres premiers p.

Nous nous intéressons à la période de l'expansion décimale de 1/p.

Voici ce que cela donne pour les premiers nombres premiers:

P	1/P	S.Ch.
2	0,5	/
3	0,3	/
5	0,2	/
7	0,142857	27
11	0,09	9
13	0,076923	27
17	0,0588235294117647	72
19	0,052631578947368421	81
23	0,0434782608695652173913	99
29	0,0344827586206896551724137931	108
31	0,032258064516129	54
37	0,027	9
41	0,02439	18
43	0,023255813953488372093	90

Notez que la somme des chiffres de la période est divisible par 9. Voir Brève 57-1124

Définitions

NOMBRES PREMIERS UNIQUES

Nombres pour lesquels aucun autre nombre premier n'a la même longueur de période (2 et 5 exclus) que lui.

Propriétés

Il en existe seulement 23 inférieurs à 10¹⁰⁰

On en connaît actuellement une cinquantaine.

Étudiés pour la première fois en 1980 par Samuel Yates.

Anglais

Unique prime

A prime p ≠ (2, 5) is called unique if

there is no other prime q such that

the period length of the decimal expansion of its reciprocal, 1 / p,

is equivalent to the period length of the reciprocal of q, 1 / q.

Liste des nombres premiers uniques

Longueur de la période	Premier unique	Période
1	3	3
2	11	0, 9
3	37	0, 2, 7
4	101	0, 0, 9, 9
9	333 667	0, 0, 0, 0, 0, 2, 9, 9, 7
10	9 091	0, 0, 0, 1, 0, 9, 9, 9, 8, 9
12	9 901	0, 0, 0, 1, 0, 0, 9, 9, 9, 8, 9, 9
14	909 091	0, 0, 0, 0, 0, 1, 0, 9, 9, 9, 9, 9, 8, 9
19	1 111 111 111 111 111 111	018 , 9 (avec 18 "0" en tête)
23	11 111 111 111 111 111 111 111	022 , 9
24	99 990 001	07 , 9, 9, 9, 9, 9, 9, 9, 8, 9, 9, 9, 9
36	999 999 000 001	011 , 1, 0, 0, 0, 0, 0, 0, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 9, 9, 9, 9, 9, 9
38	909 090 909 090 909 091	017 , 1, 0, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 9
39	900 900 900 900 990 990 990 991	023 , 1, 1, 0, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 8, 9
48	9 999 999 900 000 001	015 , 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 9, 9, 9, 9, 9, 9, 9, 9
62	909 090 909 090 909 090 909 090 909 091	029 , 1, 0, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 9
93	900 900 900 900 900 900 900 900 900 900 990 990 990 990 990 990 990 990 990 991	059 , 1, 1, 0, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 8, 9
106 120 134 150 196 294 …	…	…

Programmation – Extraction de la période
	Commentaires Exemple avec 333 667. La première instruction extrait le quatrième élément de l'expansion décimale de 1/n; c'est la période. L'instruction nops donne la quantité d'éléments. La boucle suivant compte la quantité de zéros en tête de la période. Affichage en bleu de la période, de la quantité de chiffres dans la période et de la quantité de "0" en tête.

Voir Programmation – Index

Suite	Nombres de type premier
Voir	Premiers – Index
Site	OEIS A007615 – Primes with unique period length
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremUniq.htm