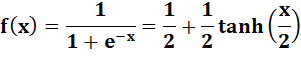|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
EN TRAVAUX
|
Courbe en S, sigmoïde tangente hyperbolique Comment approcher
une courbe en S avec des fonctions polynomiales. Le but étant de calculer une
telle fonction avec les seules quatre opérations. |
|
|
||
|
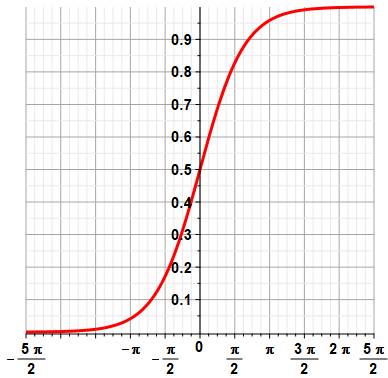
Tangente hyperbolique de -5Pi/2 à
5Pi/2
|
Idem de -Pi à Pi
|
|
|
|
||
|
Fonction |
|
|
|
Courbe représentative |
|
|
|
Au voisinage de x = 0 avec la droite
de pente 1/4 (en vert). Au voisinage de 3Pi f = 0,999919… avec la droite asymptote: y = 1 (en bleu). |
|
|
|
|
||||
|
Première approche Le but
est d'obtenir une courbe en S dans une zone limitée autour de x = 0. Comment
s'en approcher avec une fonction polynomiale ? Avec
GeoGebra (logiciel gratuit), vous pouvez composez vos courbes. Vous
écrivez simplement l'équation dans la zone de saisie.
et
vous obtenez immédiatement le graphe de droite (centré sur l'origine). |
La
fonction en y = x3 se rapproche le plus de la fonction
sigmoïde au voisinage de x = 0
|
|||
|
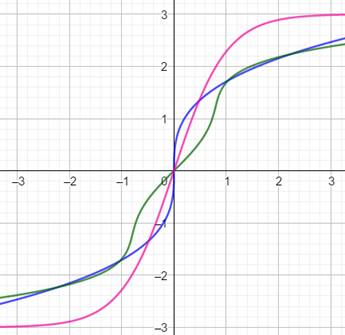
Deuxième approche On
poursuit nos recherches avec la fonction en x3 pour atteindre une
approximation de 5 tanh (x) (en vert) par la fonction (représentée en bleu); Valable
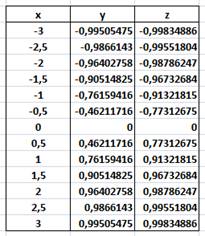
pour x de -2,5 à 2, 5. Méthode pour trouver cette fonction Sur un
tableur:
Courbe de tendance Tracer le nuage de
points (pas la courbe !) avec x et z. |
|
|||
|
Demander une courbe
de tendance en cochant équation et coefficient (de qualité de
l'approximation) L'équation est indiquée. Ci-dessus, elle a été adaptée avec un facteur
d'échelle pour améliorer la présentation. |
|
|
||
![]()
|
Bases |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/TanHyper.htm
|
![]()