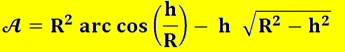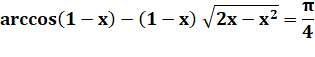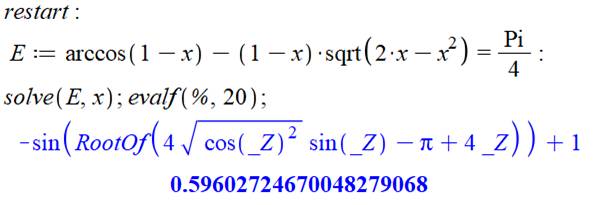|
Édition du: 01/03/2024 |
|
INDEX |
Énigmes de remplissage |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
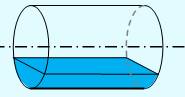
Citerne au quart remplie
La
citerne cylindrique est remplie au quart de sa capacité. Quelle est la hauteur
de liquide lorsque la citerne est en position horizontale ? Pour un
remplissage au quart, la hauteur de liquide est 0,596… R. |
||
|
|
Sommaire de cette page >>> Problème du remplissage de la citerne >>> Quart de citerne >>> Résolution par tableur >>> Résolution avec GeoGebra >>> Résolution avec logiciel >>> Abaque: coefficient de remplissage >>> English corner |
Débutants Glossaire |
Anglais: Quarter-Tank Problem
|
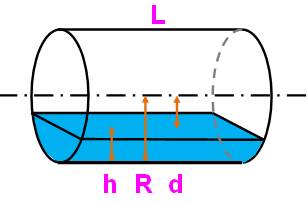
Problème direct Une citerne cylindrique est en position
horizontale. Elle contient du gazole. La jauge indique h = ¼ du diamètre du cylindre.
Quelle est la quantité de gazole ? Le volume est égal à la longueur du cylindre
multiplié par la section qui est ici un segment
de disque A. Problème inverse Nous devons verser une quantité connue de gazole dans
la citerne. Quelle est la hauteur h à
atteindre ? Ce problème n'a pas de solution analytique. Pas de
formule de calcul. Certes, une équation, mais pas possible de la résoudre
sans approximations. |
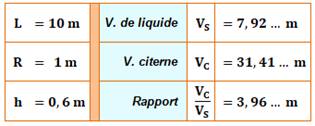
Exemple
|
|
Voir Brève
58-1146

|
Problème de la citerne remplie au
quart Si L est la longueur du segment, S est l'aire du
segment et C celle du disque, le problème consiste à résoudre S٠L = C٠L/4 ou plus
simplement S = C/4. Du fait de la présence de l'arccos cette équation
n'a pas de solution directement calculable. On utilise un calcul par approximations
successives. Solution Ce cas particulier du quart de capacité est classique
et la valeur de h est répertoriée dans l'encyclopédie des nombres en OEIS
A133742. Équation à résoudre avec x = h/R
|
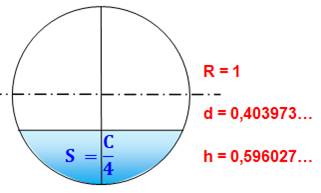
h = 0,596027246700482790681… A = C/4 = π/4 =
0,7853981635… |
|
Voir Arccos
ou cos-1
|
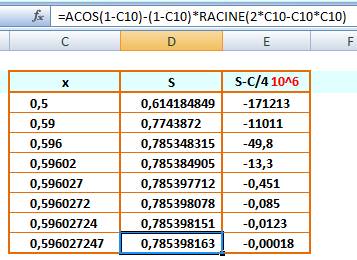
Méthode La valeur de x est entrée dans la colonne x. La
valeur de l'aire du segment est en colonne S. La colonne de droite indique la
proximité avec le résultat attendu, ici Pi/4. La formule de calcul pour S est montrée dans
l'en-tête. La méthode consiste à donner une valeur initiale
de x. On arrive vite à x compris entre
0,5 et 0,6. On cherche le chiffre suivant tel que l'écart est
négatif alors que 1 de plus engendre un écart positif. Le tableur permet d'arriver à une précision de
neuf chiffres. |
|
|
Voir Tableur
|
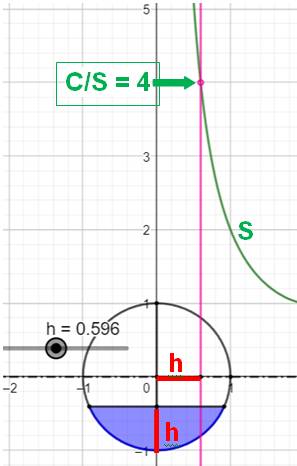
Méthode Sur la figure en bas, on observe le niveau de
remplissage pour une hauteur h. Celle-ci est définie par un curseur dont on peut
faire varier la valeur. Lorsque la valeur croit le niveau du liquide
augmente. Le curseur positionne également la droite verticale
rose. Celle-ci coupe la courbe verte qui est la représentation du rapport de
l'aire du disque à celle du segment. Le curseur est ajusté pour que l'intersection se
produise pour le rapport 4. La valeur h = 0,596 produit cet effet. La précision peut être augmentée en limitant la
dynamique du curseur et en zoomant sur le point d'intersection. Cette méthode permet de trouver d'autres valeurs
de jauge pour d'autres rapports entre les aires (ou les volumes pour le cas
du cylindre). |
|
|
Voir GeoGebra
|
Maple Un logiciel de calcul comme Maple calcule immédiatement la
solution (ici, avec vingt décimales).
Note: RootOf représente les solutions d'une équation, y
compris lorsque l'équation est
transcendante, ce qui est le cas des fonctions trigonométriques. |
|
|
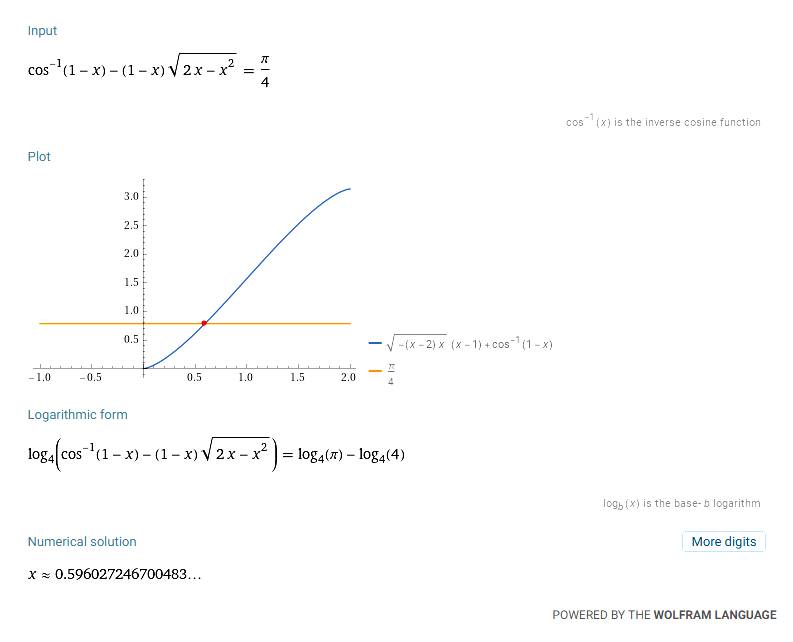
Wolfram – Online Equation Solver Logiciel de calcul disponible sur le Net en: https://www.wolframalpha.com/calculators/equation-solver-calculator
1)
Entrer l'équation dans la fenêtre
2)
Résultat du calcul
|
|
Abaque
(x est le rapport de remplissage)
avec courbe d'approximation linéaire
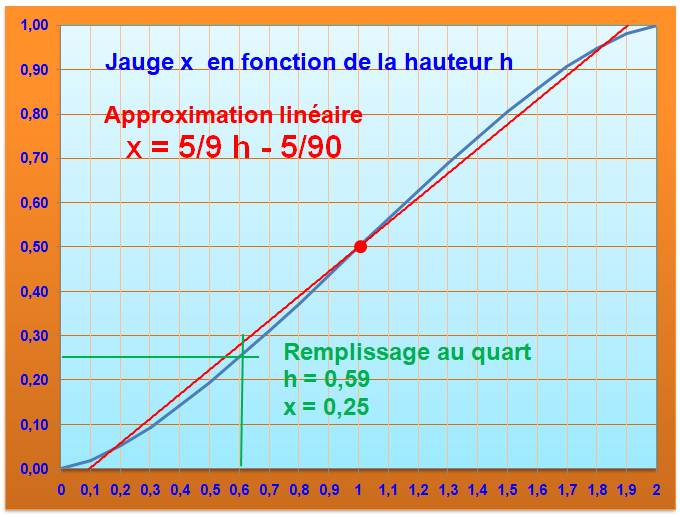
Note: Lorsque
la hauteur vaut 1 (soit le rayon), la citerne est à moitié pleine.
|
The Quarter-Tank Problem can be formulated like
this: finding the height above the bottom of a horizontal cylinder (such as a
cylindrical gas tank) to which it must be filled for it to be one-quarter
full. If the tank has a radius R, then you could
at least get the value for a half full tank would be a depth of R. But what
about 1/4th of a tank? What about 3/4th of a tank? |
Voir
Anglais pour le bac et pour les affaires
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |