Trois cercles tangents deux à deux

Édition du: 04/08/2025

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Trois cercles et longueur
	Cercle dans le triangle	Quatre cercles et un quart	Huit cercles
	Cercle et demi-cercles	Cercle et trois points	Trois cordes

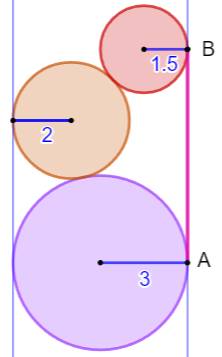
Trois cercles et une longueur

Trois cercles de rayons connus sont inclus dans un rectangle et ils sont tangents deux à deux. Calculer la longueur entre deux points de tangence.

Occasion d'un exercice de programmation Python montrant comment traiter les nombres rationnels et les nombres décimaux.

Sommaire de cette page

>>> Problème

>>> Programmation Python: calcul rationnel

Débutants

Géométrie

Glossaire

Géométrie

Problème		haut
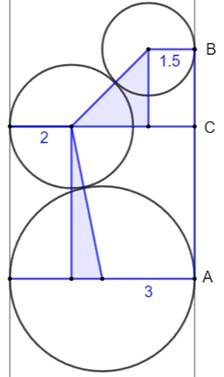
Construction Trois cercles de rayon: 3, 2 et 3/2. Tangents deux à deux. Présentant des points de tangente avec les côtés du rectangle. Question Quelle est la longueur du segment AB réunissant les deux points de tangence ? Pistes (figure de gauche en bas) Quelques tracés complémentaires et deux triangles rectangles sont matérialisés. Occasion d'appliquer deux fois le théorème de Pythagore.
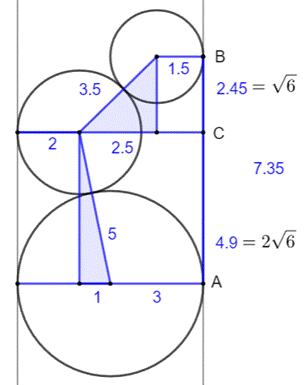
Calculs
Figure avec notations	Figure avec longueurs calculées

Programmation Python: calcul rationnel

haut

Programme

from sympy import sqrt, Rational

# Valeurs comme des rationnels

r1 = Rational(3); r2 = Rational(2)

r3 = Rational(3, 2)

# Calculs symboliques

h1 = sqrt((r1+r2)**2 - r1-r2)**2)

h2 = sqrt((r2+r3)**2 -(2*r1-r2-r3)**2)

h = h1 + h2

# Affichage

print("h1 =", h1); print("h2 =", h2)

print("h =", h)

print("h décimal =", h.evalf())

Résultats

h1 = 2*sqrt(6)

h2 = sqrt(6)

h = 3*sqrt(6)

h décimal = 7.34846922834953

But

Calculer la longueur AB tout en maintenant les valeurs intermédiaires rationnelles. Ne donner la valeur décimale qu'en fin de traitement.

Commentaires

Utilisation de Rational ( = fraction) de sympy pour réaliser les calculs sous forme symbolique.

Rational(3, 2) = 3/2

Sans cet artifice, avec r3 = 3/2, le logiciel aurait développé 3/2 en décimal et aurait calculé h2 directement en décimal. Nous n'aurions pas eu la possibilité d'ajouter les racines de 6.

Notez que le logiciel effectue les simplifications des valeurs sous radicaux:

h1 = √24 devient 2√6.

Voir Programmation – Index / Programmes Python – Index

Haut de page

Retour	Autres défis Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Résolution LLL du triangle Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CerTroiL.htm