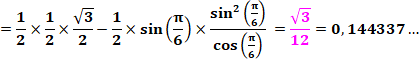Aire du quadrilatère dans le quart de cercle

Édition du: 08/10/2024

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Cercle et trg rectangle	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Trois triangles réunis
	Fourmi sur un pavé	Cercle et demi-cercle	Défis divers
	Cercle sur équerre	Cercle et quart de cercle	Demi-cercle – Divers

Quart de cercle

Quelle est l'aire d'une tranche de quart de cercle ?

Quelle est l'aire du quadrilatère ?

Un problème qui montre l'importance des constructions complémentaires.
En passant, une belle application du théorème de Ptolémée.

Sommaire de cette page

>>> Tranches de quart de cercle

>>> Quadrilatère et triangles semblables – Méthode 1

>>> Quadrilatère cyclique et théorème de Ptolémée – Méthode 2

Débutants

Géométrie

Glossaire

Géométrie

Tranches de quart de cercle

haut

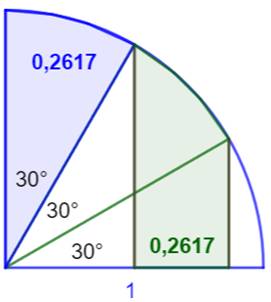
Construction

Un quart de cercle dont l'arc est divisé en trois parts égales.

Perpendiculaires aux points d'intersection par rapport au côté du quart de cercle.

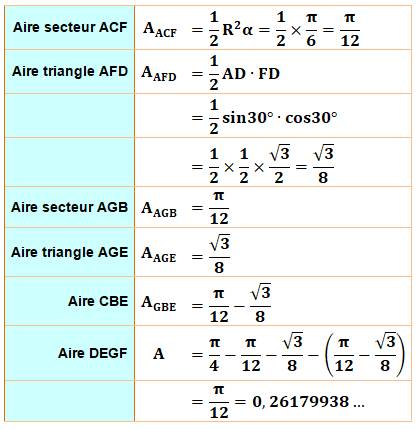
Montrer que la surface verte est égale à la bleue.

Piste et calcul

L'aire de la tranche verte est égale à l'aire du quart de cercle diminué de la tranche gauche et de la tranche droite.

Chacune met en jeu un secteur de disque dont l'aire est connue.

On en déduit aussi que: aire AHF = aire DEGH

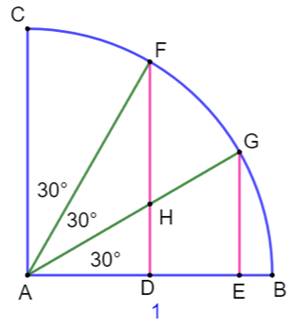
Figure initiale

Notations

Calcul de HD avec les triangles semblables ADH et AEG: AD/DH = AE/EG

Méthode 1 – Quadrilatère et triangles semblables		haut
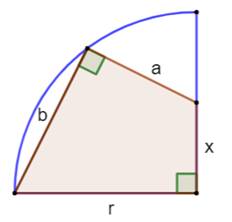
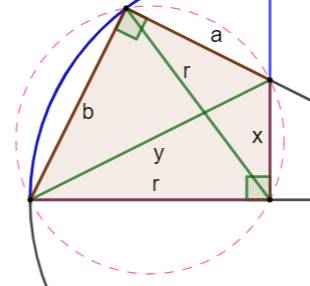
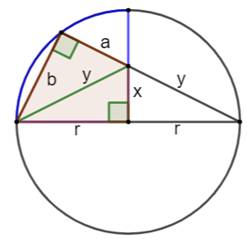
Construction (figure du haut) Un quart de cercle. Un angle droit inscrit dont les côtés limités par le quart de cercle mesurent a et b. Quelle est l'aire du quadrilatère coloré ? Observations (figure du milieu) Comme souvent en maths, il faut imaginer des constructions complémentaires et, même parfois, dépasser le cadre. Ici, notamment, l'angle droit en présence d'un cercle fait penser qu'il intercepte un diamètre du cercle. On construit donc le cercle complet et les quelques segments indiqués. 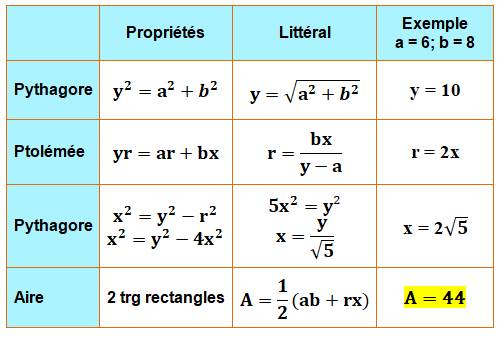Le diamètre vaut 2r, et sur lui est construit un triangle isocèle dont les côtés valent y. 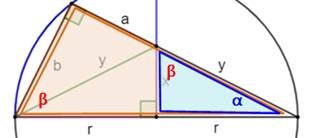De plus, avec le théorème de Pythagore: y² = a² + b² = x² + r² Triangles semblables (figure du bas) Les deux triangles colorés sont semblables. En effet: angle alpha commun, et angle droit pour chacun. Pour info, les angles bêta sont complémentaires avec l'angle alpha, ils sont donc égaux. Avec des triangles semblables, les proportions des côtés sont respectées: homothétie.
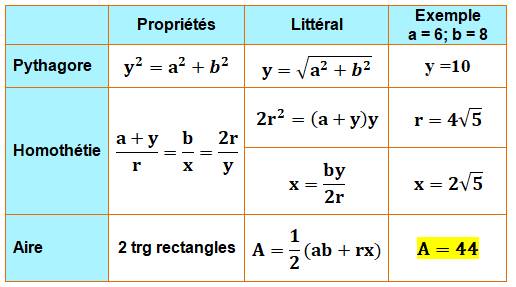
Calculs

Méthode 2 – Quadrilatère cyclique et théorème de Ptolémée		haut
Points cocycliques Le quadrilatère coloré est formé de la juxtaposition de deux triangles rectangles, chacun est inscrit dans un demi-cercle: les quatre sommets sont cocycliques. Le quadrilatère est cyclique. Théorème de Ptolémée Ce théorème dit que, dans un quadrilatère cyclique, le produit des diagonales est égal à la somme des produits des côtés opposés: yr = ar + bx Ce problème comporte trois inconnues: x, y et r. On dispose de trois équations: théorème de Ptolémée dans le quadrilatère; théorème de Pythagore dans le triangle rectangle aby; et théorème de Pythagore dans le triangle rectangle xry.	Le quadrilatère cyclique Quatre sommets sur un cercle (en pointillé).
Calculs

D'après Right Angle Inside A Quarter Circle – Mind Your Decision – Presh Talwalkar

Retour	Autres défis Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CerQuart.htm