Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 30/01/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Défis divers
	Trois triangles réunis	Cercle et demi-cercle	Cercle et quart de cercle
		Cercle et demi-cercles	Demi-cercle – Divers

Cercles et demi-cercle
	Sommaire de cette page >>> Cercle et demi-cercle dans demi-cercle	Débutants Géométrie Glossaire Géométrie

Cercle et demi-cercle dans demi-cercle		haut
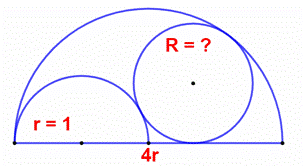
Avec deux demi-cercles emboîtés, l’un moitié de l’autre en diamètre, quel est de rayon maximum du cercle remplissant l’espace libre ? Résolution classique avec Pythagore.
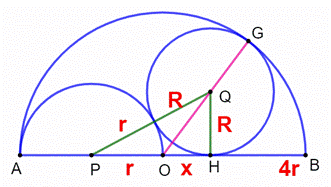
Construction Un demi-cercle de diamètre 4r. Un demi-cercle dont le rayon (r = 1) s’aligne sur le diamètre du plus grand. Un cercle complet (rayon R) remplit l’espace libre avec trois points de tangence. Relation entre R et r ? Pistes Dans le triangle rectangle OHQ : Sachant que OG = 2r (2r – R)² = x² + R² 4r² – 4Rr + R² = x² + R² x² = 4r² – 4Rr Dans le triangle rectangle PHQ : (R + r)² = R² + (r + x)² R² + 2Rr + r² = R² + r² + 2rx + x² 2Rr = 2rx + x² En remplaçant 4Rr par sa nouvelle valeur : x² = 4r² – 4Rr = 4r² – 4rx – 2x² 3x² + 4rx – 4r² = 0 Passage en numérique avec r = 1 : 3x² + 4x – 4 = 0 Racine positive : x = 2/3 Calcul de R x² = 4r² – 4Rr => 4/9 = 4 – 4R R = 1 – 1/9 = 8/9	Figure initiale Figure avec notations Solution générale

Haut de page

Retour	Autres défis Géométrie – Index Énigmes – Index Brèves – Index
Suite	Quadrilatère dans le quart de cercle Divers défis 02 Équation en x^4 Résolution LLL du triangle Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CerclMi2.htm